在上一个话题中,我们介绍了两种常见的MPPT算法,即观察扰动法(Perturb and Observe,P&O)和电导增量法(Incremental Conductance,INC),具体内容请看MPPT基本算法介绍。在本话题中,我们将介绍MPPT算法中一个常见的问题,即步长设计。
定步长算法
MPPT算法在运行时,主要分为两个阶段:当由于光照变化而导致工作点远离MPP时,MPPT算法需要重新追踪新的MPP,此过程被称为动态阶段(dynamic stage);而当MPPT算法找到MPP时,MPPT算法需要在MPP处进行扰动,这一过程则被称为静态阶段(steady-state stage)。而MPPT算法的扰动步长(此处,我们将其简称为步长),将决定动态阶段和静态阶段的追踪效率 [1]。
当MPPT算法使用两种不同的步长时,其动态效率与静态效率如下图示:
当MPPT算法采用较小步长时,在静态阶段,MPPT算法在MPP处扰动较小,如A-B-C所示,故而静态效率较高;但是,在动态阶段,由于步长较小,因此动态追踪速度较低,故而动态效率较低。
同理,当MPPT算法采用较大步长时,其动态效率较高,但静态效率较低。
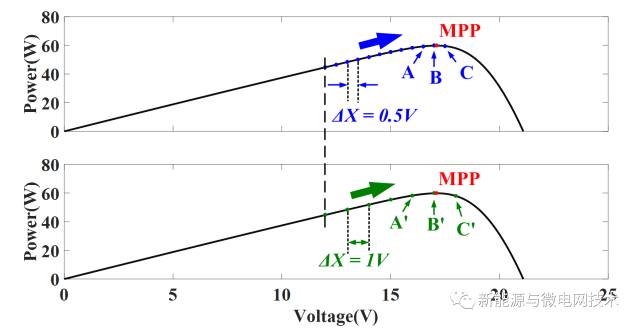
从上述分析中,不难看出,对于步长的大小,我们要进行一定的取舍(tradeoff)。由于上述MPPT算法的步长为定值,因此此类方法一般被称为定步长MPPT算法。
变步长算法
为了解决这一问题,变步长MPPT算法现已被提出并被广泛地应用。
变步长算法一般是根据P-V曲线的斜率,即ΔP/ΔV的大小,来对步长进行调节的,一般可由以下公式得出 [2]:
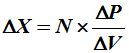
其中,ΔX为步长,N为步长比例系数。
如下图所示,当工作点离MPP较远时,其ΔP/ΔV较大,故而步长较大、动态追踪速度较快;而当工作点离MPP较近时,其ΔP/ΔV较小,故而步长较小、静态扰动幅度较小。因此,只要设定好步长比例系数N,MPPT算法就可以调节步长大小。
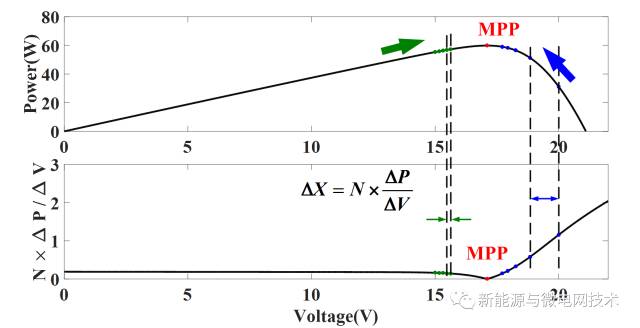
但是,如何设定步长比例系数N,则是另一个问题。具体分析如下图示:
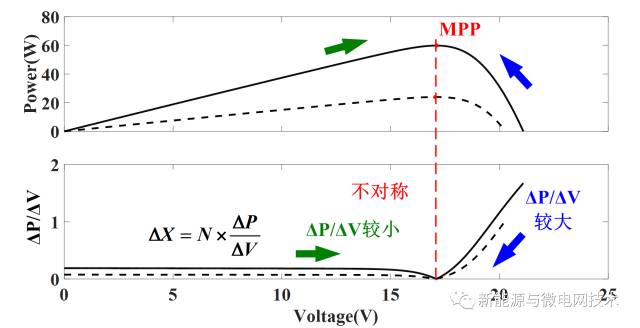
在同意光照、温度的情况下,在MPP左侧的ΔP/ΔV较小,而在MPP右侧的ΔP/ΔV较大。如果N值设定较小,则会导致步长在MPP左侧时较小,从而影响动态效率;如果N值设定较大,会导致步长在MPP附近较大,从而影响静态效率。同时,在不同光照、温度的情况下,这种不对称则会进一步加剧。
此外,在不同光照的情况下,即使在MPP的同一侧,其ΔP/ΔV的大小也不尽相同。同理,如果N值设定较小,则会影响其在低光照下的动态效率;而如果N值设定较大,则会影响其在高光照下的静态效率。
综上所述,我们在设计变步长MPPT算法时,则要对步长比例系数N进行一定的取舍。因此,此类算法并不够完美。
混合步长算法
为了解决这一问题,混合步长MPPT算法在最近几年内被提出并应用。其算法的基本思路为:在远离MPP时,采用变步长;而在MPP附近时,采用定步长。其代表作为Beta法、MPP-Locui法、ZA-PO法等。现以Beta法为例,进行一个初步的介绍 [3,4]。
如下图所示,Beta法首先将整个P-V曲线分为两部分:一部分在βmin和βmax的范围内,而另一部分则在此范围外。其中,β的值可以由以下公式求得:
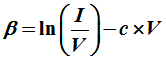
其中,c值为一个常数,可以通过c=q/(NsAKT)来求出。而βmin和βmax的范围则可根据光伏组件的参数来进行设定。具体细节详见文献。
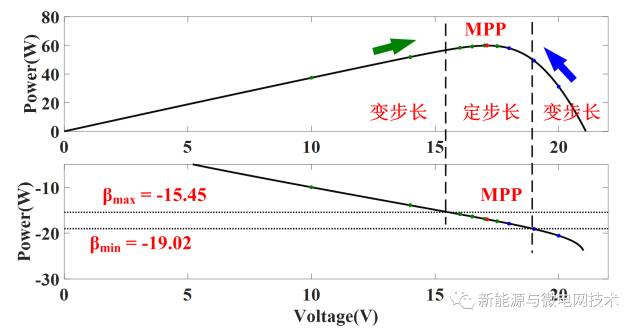
如上图所示,当工作点在βmin和βmax的范围外时,Beta法使用变步长;而当工作点在βmin和βmax的范围内时,Beta法使用定步长。这一种将变步长与定步长混合起来的算法,显然不需要进行过多的取舍,因此动态与静态效率可以同时满足。









暂无评论