1.数字信号处理原理

        线性系统中，信号只能以乘以一个常数之后再相加的方式进行组合。例如，一个信号不能直接乘以另外一个信号。如下图所示，根据给出三个信号：x0[n],x1[n],x2[n]相加得到最终的信号x[n]。通过相乘和相加的形式进行信号的组合被称为信号的合成。

与信号合成相反的步骤，叫做信号的分解。即把原始信号分解为两个或多个信号相加。信号的分解要比信号合成要复杂些。试想，假设我们把15和25相加，那么我们只能得到40,；相反，如果我们把40分解成两个或多个数字的相加，那么这种分解会有无数种形式，比如1+39,2+38，-30.5+60+10.5。

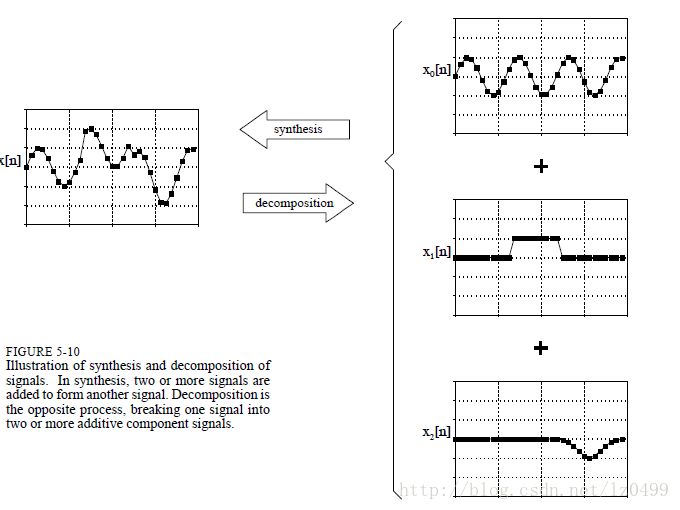
图1

        数字信号处理中，最为关键的步骤是信号的叠加。假设有如下图的输入信号x[n]，经过一个线性系统之后，输出信号为y[n]。输入信号可以分解为多个更为简单的信号：x1[n],x2[n],x3[n]，这些被称为输入信号分量。之后把各个输入信号分量单独的输入到线性系统中，产生与之对应的输出信号分量：y1[n],y2[n],y3[n]。原始的输入信号经过线性系统之后，得到的输出信号y[n]即为各个输出信号分量的合成。线性系统中，通过这种方式获得的输出信号和原始信号直接通过系统得到的输出结果是一样的。正因为如此，任何复杂的数字信号，我们应该把它分解为更为简单的输入信号分量，经过线性系统后把输出信号分量进行合成即为最终的输出信号。但是，如果分解的输入信号不够简单，那么这样与分解之前的效果是一样的，需要复杂的计算。

     假设你需要计算2014乘以4的结果，我们可以这样进行计算：把2014分解为2000+10+4，分解的系数分别乘以4再相加即为最终的输出结果。这种方法比直接把两个数相乘要简单得多。

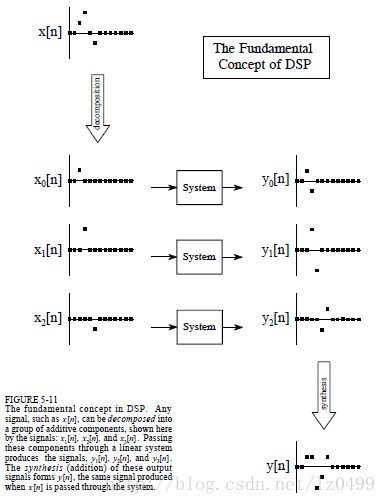
图2

2.卷积

脉冲分解

    脉冲分解是卷积的基础。如下图所示，N个采样信号经过脉冲分解之后，形成N个信号分量，每个信号分量只包含原始信号的某一个采样点信号，而其他采样点的值为0。假若某个信号只有一个非零点，其他各点数值均为0，那么这个信号被称为脉冲信号。

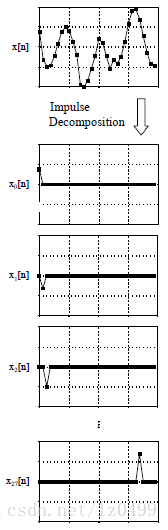
图3

脉冲函数

     Delta函数用希腊字母表示为o[n]。delta 函数是一个归一化的脉冲信号，即在采样点零点位置其值为1，其他采样点位置各点数值均为0。

脉冲反应

     当线性系统中输入信号为delta函数时，其输出的信号称为脉冲反应。如下图所示。如果两个不同的线性系统，当输入信号均为delta函数时，其输出分脉冲反应也是不同的。就像离散数字信号中，用x[n]、y[n]分别表示输入信号和输出信号，脉冲反应使用h[n]表示。当然，你也可以使用其他的符号表示，比如f[n]等。

   任何脉冲信号都可以看作是脉冲函数的平移和缩放。例如，假设信号a[n]只在采样点8的位置有输入，且其输入值为-3，这就相当于把delta函数平移到8的位置，在乘以-3.用公式表示为：a[n] = -3 o[n-8]。假如delta函数的脉冲反应为h[n],那么a[n]的脉冲反应为-3h[n-8]。

    卷积就像数学的加减乘除一样，是一种形式化的数学运算。数学运算中输入两个数得到第三个数，卷积则是输入两个信号产生第三个信号。卷积被广泛应用于统计和概率中。在线性系统中，卷积描述的是输入信号，脉冲反应和输出信号三者之间的关系。

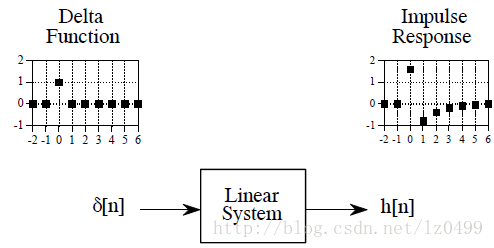
图4

     上图描述的是卷积应用于线性系统的示意图。输入信号x[n]进入有脉冲反应h[n]的线性系统，产生输出信号y[n]。用公式表示为:x[n]*h[n] = y[n]。

3.卷积运算

      卷积可以从输入信号的角度理解：输入信号的每一个采样点是如何贡献于多个输出信号采样点，即每一个输入信号分量进入线性系统之后，都将产生多个平移和缩放版本的脉冲反应，输出结果即为每个信号分量对应的平移和缩放版的脉冲反应进行合成；从输出信号的角度理解：每一个输出信号的采样点是如何从众多输入信号采样点获取信息。即对于每一个输出信号，都将由多个输入信号贡献其脉冲响应，输出结果即为对应脉冲响应的线性加权。

    这两个理解只是对卷积运算的不同角度的理解，其结果都是一样的。

从输入信号的角度理解

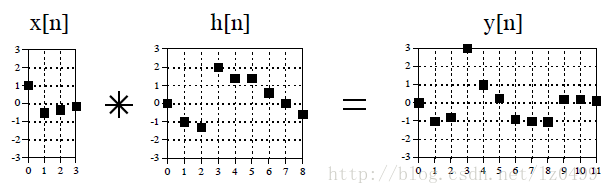
图5

       上图是一个简单的卷积计算。输入信号x[n]有九个点，输入一个有四个脉冲反应h[n]的线性系统中，得到9+4-1输出信号y[n]。用数学术语表示为：x[n]卷积h[n]输出结果y[n]。以第一种角度理解卷积：分解输入信号，把输入信号分量通过线性系统，然后把每一个输出分量进行合成。在这个例子中，输入信号的每一个采样点都将产生一个平移和缩放版的脉冲反应，输出信号即把这些平移和缩放版的脉冲反应叠加生成最终的输出信号y[n]。其具体的计算过程如下图所示：

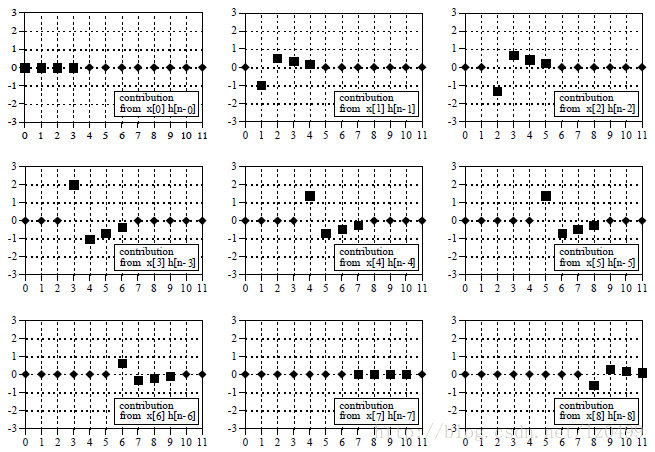
图6

                           图6：输入信号中的每一个分量都将产生一个平移和缩放版的脉冲反应。即用方形所表示的脉冲反应结果。除了方形之外的所有点起数值均为0.

       假设我们从输入信号的第四个采样点x[4]开始。这个采样点的下标为4，其值为1.4。当输入信号分解之后，这个采样点可以用脉冲函数表示为：1.4 o[n-4]。经过线性系统之后，该采样点所对应的输出信号分量为1.4h[n-4]。如上图中间位置图像所示。注意到输出信号分量脉冲反应乘以1.4，并把采样点右移到下表为四的采样点。0-3,8-11各点数值均为0.

      上图中方块形状表示的即为平移和缩放的脉冲反应数值，钻石形状的点其值为0.

     当输入信号是四个采样，经过有九个点的脉冲反应线性系统，其输出的结果与上图所示的方法结果相同。

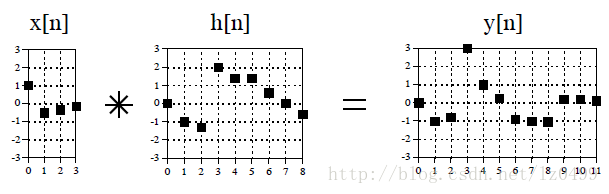
图7

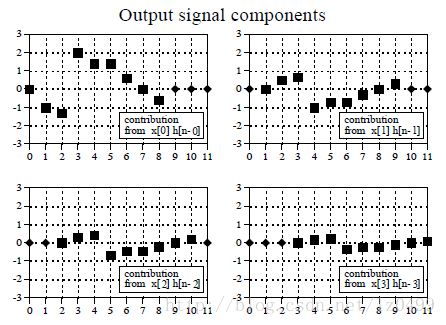
图8

     上述两种计算方法结果相同，揭示了卷积的一个重要性质：卷积的交换律。即a[n]*b[n]=b[n]*a[n]。即卷积并不关心哪个信号是输入信号哪个信号是脉冲反应。

     假设输入信号为{1,2,3,4,1,2,3,4,5}；脉冲反应为：{2,3,1,4};则卷积计算过程相当于如下所示，每一个输入信号分量分解为单个脉冲函数，经过四个点的h[n]线性系统之后，其输出结果即为h[n]+2*h[n-1]+3*h[n-2]+4*h[n-3]+ h[n-4]+2*h[n-1-5]+3*h[n-6]+4*h[n-7]+5h[n-8]。

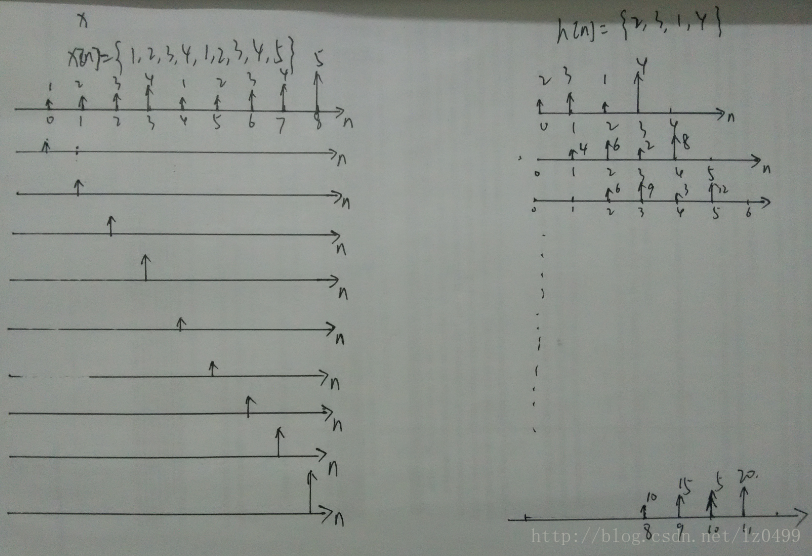
图9

图10

从输入信号角度理解卷积代码示例：

#include

#include

#include

int  main(){  int InputSignal[9] = {1,2,3,4,1,2,3,4,5};  int ImpulseCorres[4] = {2,3,1,4};  int OutPut[12] = {0};  int i,j;  //input view  for(i = 0;i < 9;i++)  {    for(j = 0;j < 4;j++)      OutPut[i+j] = OutPut[i+j]+InputSignal[i]*ImpulseCorres[j];  }    for(i = 0;i < 12;i++)  {      printf("%d ",OutPut[i]);  }    return 0;}

从输出信号的角度理解

      从输出信号角度理解卷积，分析的是每一个输入信号的采样点是如何影响众多输出信号的采样点。而从输出角度理解卷积，分析的是输出信号的每一个采样点是由哪些输入信号影响的。这种方式对数学角度和实践应用角度理解卷积都相当有作用。用公式表示即为：y[n]=其他变量的组合。换句话说，输出信号采样点n等于众多输入信号和脉冲反应的线性组合。

     从如图6可以看出，单个输出信号是如何受到众多输入型号的影响的。假设我们以y[6]为例，在图6中找到在n=6的位置，九个输入信号中有哪些数值为非零的采样点作用于该位置。由图可以看出五个输入信号在n = 6的位置其数值为0，只有四格输入信号作用于n = 6的时候其数值不为零。分别是x[3],x[4],x[5],x[6]。y[6]的最终结果即为这四个输入信号作用单独作用于线性系统的后输出信号分量之和。即y[6] = x[3]*h[3]+x[4]*h[2]+x[5]*h[1]+x[6]*h[0]。

      图11，从输出信号角度理解卷积，其相当于一个卷积机器。如图所示，假设输入信号x[n]，输出信号y[n]， 虚线方框里表示的是卷积机器，可以从左到右从右到左自由移动。卷积机器放置的位置应该与我们需要求得输出信号采样点对其，输入信号的四个采样点进入到卷积机器，四个采样点的数字分别于其对应的脉冲反应相乘，再把其乘积相加。例如为了计算y[6]，需要把x[3],x[4],x[5],x[6]四个输入信号输送到卷积机器。相应的，为了计算y[7]，卷积机器必须右移一位到采样点7的位置，这样，进入到卷积的四个信号分别是x[4],x[5],x[6], x[7],如此循环直到所有输出信号分量被计算完成。

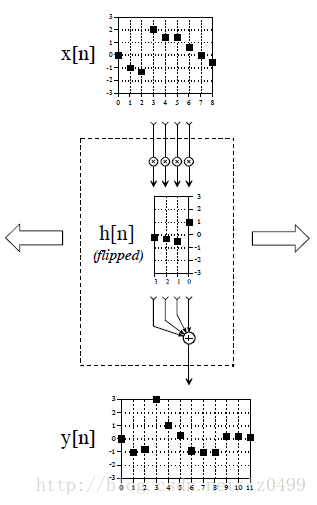
图11

     卷积机器中脉冲反应排列顺序是相当重要的。卷积机器中的脉冲反应与原始的脉冲反应做了一个镜像的翻转。为什么需要翻转呢？

     即假设我们计算y[4]的输出结果，由上图可知y[4] = x[4]*h[0]+x[3]*h[1]+x[2]*h[2]+x[1]*h[3]+x[0]*h[4]。即当前输入信号点输入到线性系统对应的输出结果是当前信号和之前各个信号对当前点的脉冲反应的一个线性加权。如公式所述，为了计算y[4]的结果，我们必须把输入x[0],x[1],x[2],x[3],x[4]作用在n = 4的位置的脉冲响应进行线性加权。也就是说，当x[0]进入系统的时候，在n = 4的位置对应的脉冲反应为h[4]，其输出为x[0]*h[4]，当x[1]进入系统后，在n = 4的位置对应的脉冲反应为h[3],其输出结果为x[1]*h[3]以此类推。由此可以看出，输出信号的每一个分量都是有收到输入信号影响的权重线性组合，其权重恰好是脉冲反应的镜像翻转对应的权重值。这也就是为什么卷积公式中需要把输入信号进行翻转在进行线性叠加的原因。

    假设有N个点的输入信号x[n],采样点从0-N-1，有M个点,脉冲反应为h[n]的线性系统，信号点从0-M-1。则这两个信号的卷积将输出有N+M-1个采样点的信号，下标从0-N+M-2。用公式表示为：

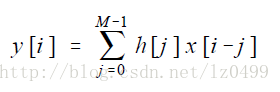
从输出信号角度理解卷积代码示例：#include

#include

#include

int  main(){  int InputSignal[9] = {1,2,3,4,1,2,3,4,5};  int ImpulseCorres[4] = {2,3,1,4};  int OutPut[12] = {0};  int i,j;  //output view  for(i = 0;i < 12;i++)  {    OutPut[i] = 0;    for(j = 0; j < 4;j++)    {      if((i-j)<0)        continue;      if((i-j)>8)        continue;      OutPut[i] += ImpulseCorres[j]*InputSignal[i-j];    }  }  for(i = 0;i < 12;i++)  {      printf("%d ",OutPut[i]);  }  return 0; }

4.图像中的卷积

    假设二维函数I和H,对应的卷积操作可以表示为：

  也可以表示为：

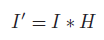
应用于图像领域时，其卷积公式也可以表示为：

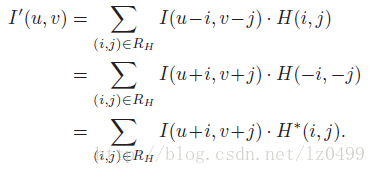
     当滤波函数H*(I,j) = H(-I,-j)进，H(I,j)进行了180度旋转之后，其结果与线性滤波时一样的。

    图像中的线性滤波可以表示为：

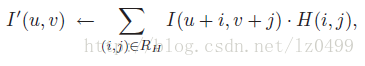
   其原理为：

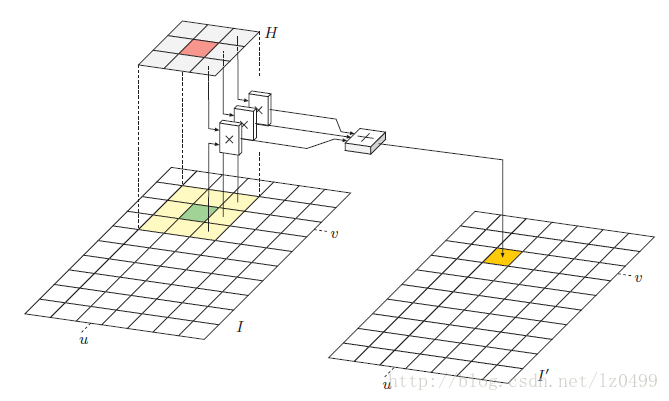
     由两者的公式可以看出，线性滤波其实是把滤波函数进行180度旋转之后进行卷积的结果。