1）关于编码的基础知识

在信息的传输过程中，为了达到更高效、更低误码的目的，不可避免地要在发送端进行编码，在接收端进行解码。

通常，编码可以分为信源编码和信道编码，具体的区分可以见下图：

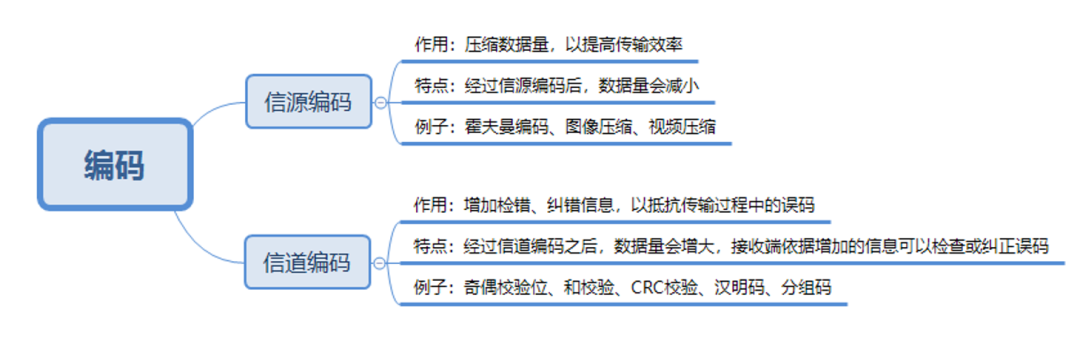
信源编码是用于压缩数据用的；信道编码是用于增加检错、纠错信息，抵抗传输误码的。

例如：奇偶校验、和校验，就是两种最简单的信道编码，在接收端，如果发现校验位/校验字节不对，就可以知道传输中出现了误码，这就是信道编码的作用。

当然，复杂一些的信道编码不只能发现传输错误，还能在一定程度上纠正传输错误。

本文中要讲的，CRC校验码和汉明码（hamming code），都属于信道编码，它们实现起来简单，效果却非常好。

常见的奇偶校验、和校验只能检出部分误码，能力有限，而CRC校验码可以检出多个bit位的传输错误，有文献表明，CRC16能100%检出：单个位误码、双位误码、奇数个误码、短于16bit的误码，能以99.99%以上的概率检出其他突发性误码。

汉明码与前面几种只能查错的编码不同，它甚至还可以纠正单个bit位的传输错误。

2）CRC校验码

首先来了解一下CRC校验码的原理。

假设我们有一串原始信息bit流要传输，从高位到低位依次为：序列1=11001100；

我们再选择一个用于生成CRC校验码的序列，假设为：序列2=100000111，总长度为k=9；我们暂时称其为“生成多项式”；

然后，我们在原始信息序列1后面增加（k-1）个0，将其和生成多项式序列2进行“模二除“（计算时不进位也不借位，二进制除法，相当于按位异或），计算过程如下：

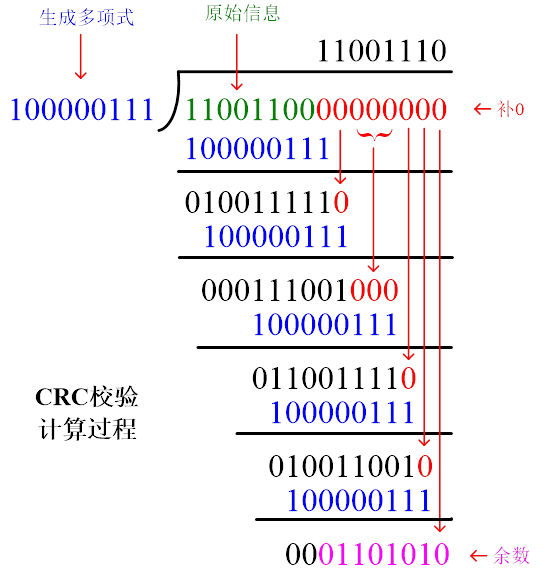
最后得到一个k-1位长度的余数（位数不够的把前面的0也算上），这个余数就是计算得到的CRC校验。

把这个余数替换到原始信息序列1后面，得到新的序列：1100110001101010，因为新的序列在末尾加上了“余数”，所以这个新的序列可以“整除”生成多项式序列2。

这样，我们只要在发送端计算出CRC校验，附加到原始信息的末尾一起发送，在接收端看能否整除，就能知道传输过程中有没有误码。

计算过程中的这个“被除数”——生成多项式，可以用多项式形式表示，也可以将序列换算成16进制表示。

计算时取的生成多项式不同，其CRC校验的结果也不同，因此，收发双方应该事先约定好生成多项式。

CRC校验的长度和生成多项式是可以自己定义的，但是一般来讲，为了通用化、标准化，一般选择8位、12位、16位或32位长度，越长它的检错能力会越强；生成多项式也有一些常用的标准形式，举几个例子如下：

注意，因为生成多项式的最高次幂决定了CRC校验的长度，多项式的最高次幂必须为1（如CRC16，多项式X^16的系数必须为1），所以在用16进制或者2进制表示时，常常省略最高位固定的1。上表中的16进制就是省略最高位1的形式。

下面给出一种C语言求CRC校验的实现方法。

我们以计算CRC8为例，生成多项式为x^8  x^2   x   1，那么它用十六进制数表示为0x107。在前面的手算示例中，我们可以发现，生成多项式的最高位是固定为1的，在循环做模二除时，每次计算的被除数的最高位也为1，所以计算完后余数的最高位必然为0，后续计算时这一位是要丢弃的。根据这个特点，我们可以省略最高位的运算，每次只算除去最高位之外的那些位的模二除法。

实现代码如下：

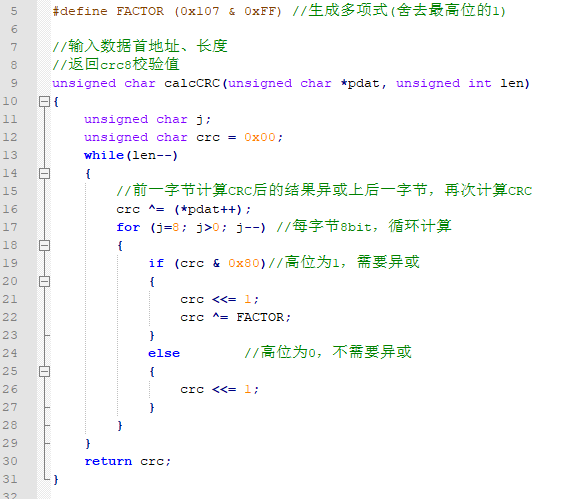
这种实现方法便于理解，和手工计算的过程相似；它的缺点在于要按bit位循环计算，每个字节要循环8次，效率很低，计算一个长串时要花费很多cpu周期。

一个加快速度的方法是查表，以空间换时间，实现过程如下所示：

查表法每个字节只用计算一次，运算速度大大提高。

可以运行上面两个函数，查看结果是否和前述手工计算的crc8值一致。

3）汉明码

汉明码的原理，是将要发送的原始信息bit位分成几组，每组算出一个校验位，再将这些校验位附加在原始信息之后传输。接收方也按同样的方法分组、计算校验，如果发现某几个校验位不对，则可以根据分组的特性找出这几个组的交集，即确定误码的bit位，然后取反就可以纠正错误了。

我们以一个简单的例子来进一步理解一下汉明码的原理：

 a)确定码长

假设我们有一串原始信息bit流要传输，长度为n，那么我们要先确定汉明码的长度（这个过程实际上等效于确定分组的组数）。

假定附加在原始信息之后的汉明码长度为m，那么编码的总长度为n m。

这n m个bit位在传输过程中，每一位都有可能误码，为了能够纠正单bit的误码，我们需要区分n m种错误状态和1种正确的状态，所以附加的m位编码，必须满足2^m ≥ (n m 1)。

假定原始信息长度n=4，那么我们可以计算出m=3时，2^3 ≥ （4 3 1）满足要求。所以我们确定汉明码长度为3（即后面我们要把原始信息的bit位分为3组计算校验值）。

（注意，当编码长度满足上述≥取到=时，编码效率最高，此时才称为汉明码）。

 b)bit位分组

接下来，我们考虑如何分组。

由于我们的目的是要使得能通过各组的交集来确定误码的bit位，那么分组方式可以如下表来确定：

 表中D1~D7表示编码后的各个bit，从表中可以看出，我们只要把C1列为1的Dx划为第1组、C2列为1的Dx划为第2组，C3列为1的Dx划为第3组，这样只要某几组的校验值出错，就能通过他们的交集来确定是哪个bit位出错。

更直观的解释如下，我们采用异或来计算校验，有：

C1 = D1^D3^D5^D7

C2 = D2^D3^D6^D7

C3 = D4^D5^D6^D7

假如计算出来的校验值C3 C2 C1 = 001，则可以确定是D1位出错了，同样地，假如计算出C3 C2 C1 = 101，则可以确定是D5位出错了，其他值也一样可以推测出来。

如果计算出C3 C2 C1 = 000，则没有单bit的误码。

可以看到，如上方式的分组，可以有效地识别出单bit的误码。

 c)确定算法

最后，我们要确定一种计算方法，使得在无误码时，计算出来的C3 C2 C1等于000。

我们观察发现，三个计算式中，D1、D2、D4都只出现了一次，所以，令C1等于0，可以求得：

D1 = D3^D5^D7

同理，令C2=0、C3=0可以求出：

D2 = D3^D6^D7

D4 = D5^D6^D7

这样，我们可以得到一个bit串：D7、D6、D5、D4、D3、D2、D1

其中D7、D6、D5、D3这几位，放原始的4bit信息，D4、D2、D1位由上式计算得到，附加在原始信息中，作为纠错码，也就是我们需要的汉明码。

实际编码实现时，D1~D7的排列顺序是可以换的，我们可以把原始信息放在前4bit，汉明码放在后3bit，只要接收方也知道这个顺序即可。

这样，我们就完成了4bit原始信息的汉明码编码。

接收端收到信息后，按照同样的分组和计算方法来获取C3、C2、C1的值，可以知道哪个bit产生了误码，如有误码，将其翻转就完成了纠正。

为了便于编码，我们把上述例子中的D3和D4调换一下位置，即D7、D6、D5、D4是原始信息位，D3、D2、D1是汉明码。

下面是这个例子的C语言实现：

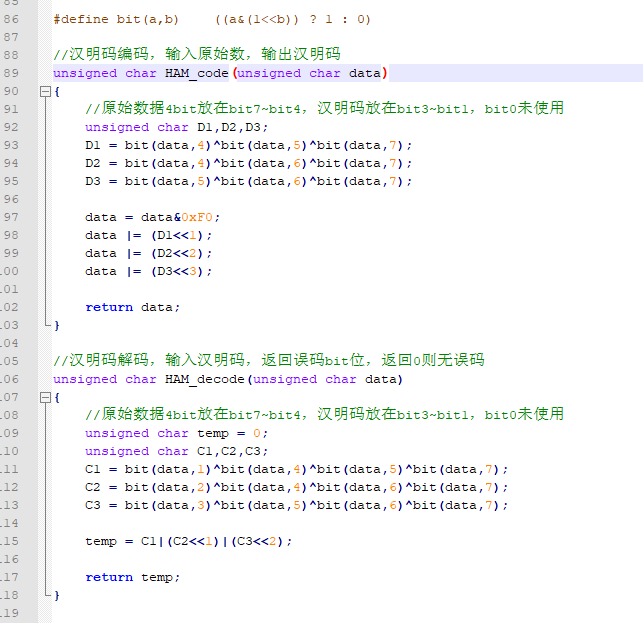
注意，这个代码中由于D3和D4的位置互换了，所以解码函数中，返回3表示的是D4出错，返回4表示D3出错，其他位的指示是一一对应的。

上述例子的汉明码实现过程可以看出，4bit信息至少要附加3bit的纠错码，效率不高；实际中，一般会选择较长的码来作为纠错码，比如：11bit信息附加4bit的纠错码，效率就要高一些。

好了，本节介绍了两种简单实用的信道编码方式，CRC校验可以检出多个bit的误码，效率较高；汉明码可以纠正单bit的误码；合理地使用它们可以大大提高通信的可靠性。