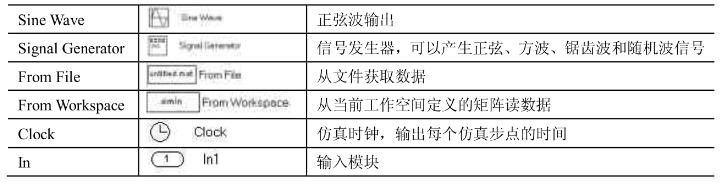
1 模糊RBF网络
在模糊系统中,模糊集、隶属函数和模糊规则的设计是建立在经验知识基础上的。这种设计方法存在很大的主观性。将学习机制引入到模糊系统中,使模糊系统能够通过不断学习来修改与完善隶属函数和模糊规则,这是模糊系统的发展方向。模糊系统与模糊神经网络既有联系又有区别,其联系表现为模糊神经网络在本质上是模糊系统的实现,其区别表现为模糊神经网络又具有神经网络的特性。模糊系统与神经网络的比较见表8-1。模糊神经网络充分地利用了神经网络和模糊系统各自的优点,因而受到了重视。
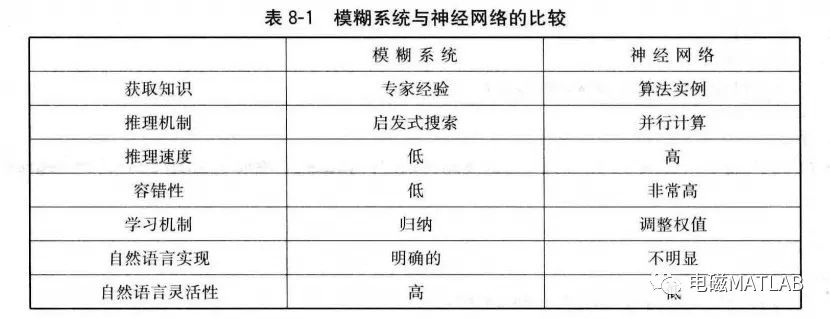
将神经网络的学习能力引入到模糊系统中,将模糊系统的模糊化处理、模糊推理、精确化计算通过分布式的神经网络来表示是实现模糊系统自组织、自学习的重要途径。在模糊神经网络中,神经网络的输入、输出节点用来表示模糊系统的输入、输出信号,神经网络的隐含节点用来表示隶属函数和模糊规则,利用神经网络的并行处理能力使得模糊系统的推理能力大大提高。模糊神经网络是将模糊系统和神经网络相结合而构成的网络。模糊神经网络在本质上是将常规的神经网络赋予模糊输入信号和模糊权值,其学习算法通常是神经网络学习算法或其推广。模糊神经网络技术已经获得了广泛的应用,当前的应用主要集中在模糊回归、模糊控制、模糊专家系统、模糊矩阵方程、模糊建模和模糊模式识别等领域。利用RBF网与模糊系统相结合,构成了模糊RBF网络。
2 网络结构
图8-1所示为模糊RBF神经网络结构,该网络由输入层、模糊化层、模糊推理层和输出层构成。
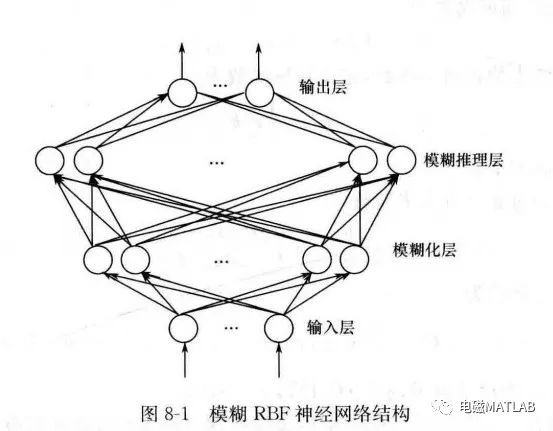
模糊RBF网络中信号传播及各层的功能表示如下:第一层:输入层该层的各个节点直接与输入量的各个分量连接,将输入量传到下一层。对该层的每个节点i的输入输出表示为

第二层:模糊化层采用高斯型函数作为隶属函数,c,和b,分别是第i个输入变量第j个模糊集合的隶属函数的均值和标准差。即
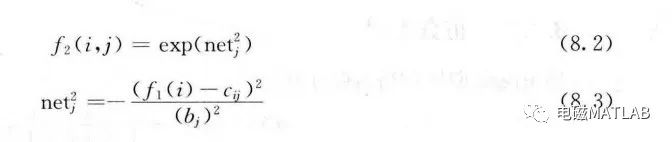
第三层:模糊推理层实现规则的前提推理,该层的每个节点相当于一条规则。该层通过与模糊化层的连接来完成模糊规则的匹配,各个节点之间实现模糊运算,即通过各个模糊节点的组合得到相应的点火强度。每个节点方的输出为该节点所有输入信号的乘积,即
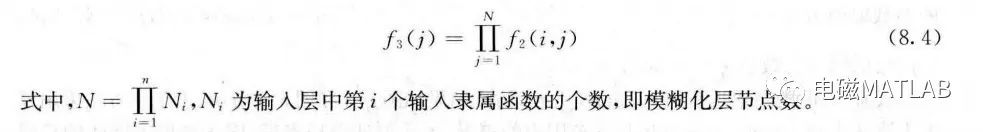
第四层:输出层实现规则前提与结论的推理及规则间的推理。输出层为f4,即
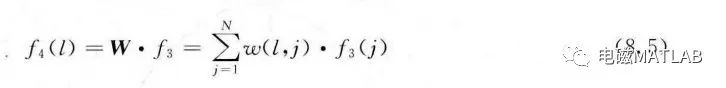
式中,L为输出层节点的个数,W为输出层节点与第三层各节点的连接权矩阵。
3 基于模糊RBF网络的逼近算法
采用模糊RBF网络逼近对象,取网络结构为2-4-1,如图8-2所示。
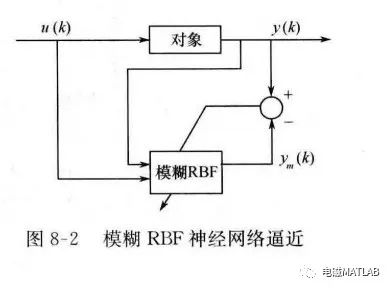
取ym()=f4,ym(k)和y(k)分别表示网络输出和实际输出。网络的输入x1和x2为u(k)和y(k),网络的输出为ym(k),则网络逼近误差为
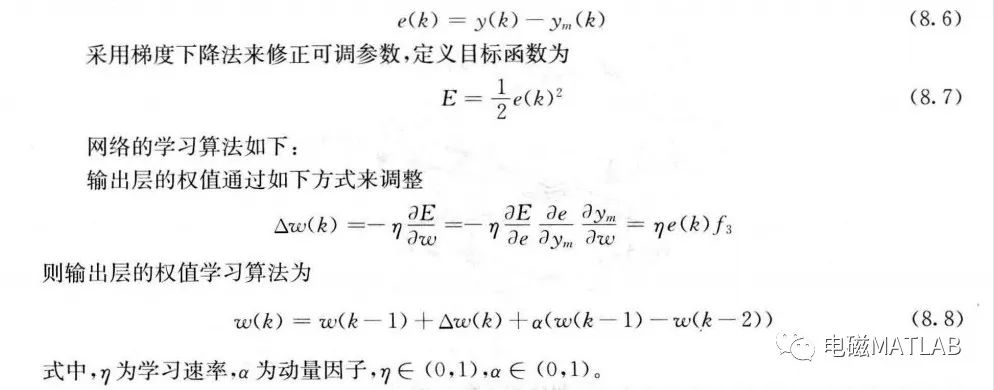
在RBF网络设计中,需要将c,和b;值的设计在网络输入有效的映射范围内,否则高斯基函数将不能保证实现有效的映射,导致RBF网络失效。如果将c,和b,的初始值设计在有效的映射范围内,则只调节网络的权值便可实现RBF网络的有效学习。
4 算例

5 matlab运行结果
1)目标轨迹
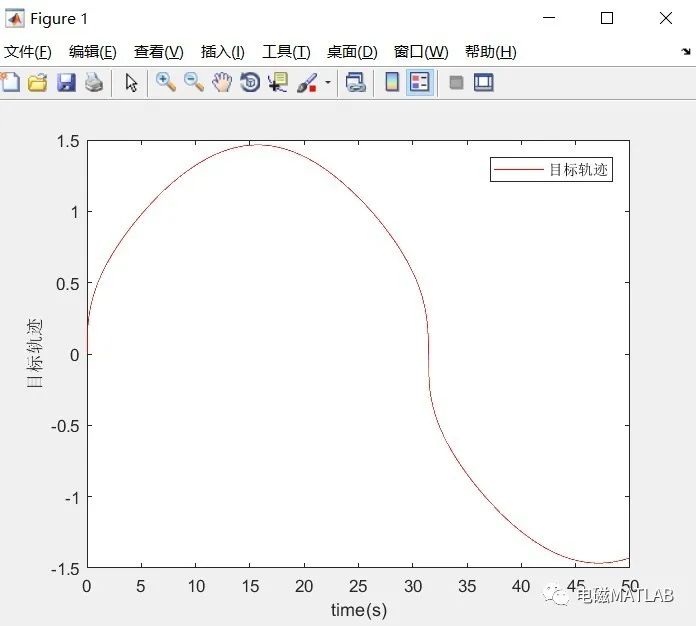
2)跟踪轨迹
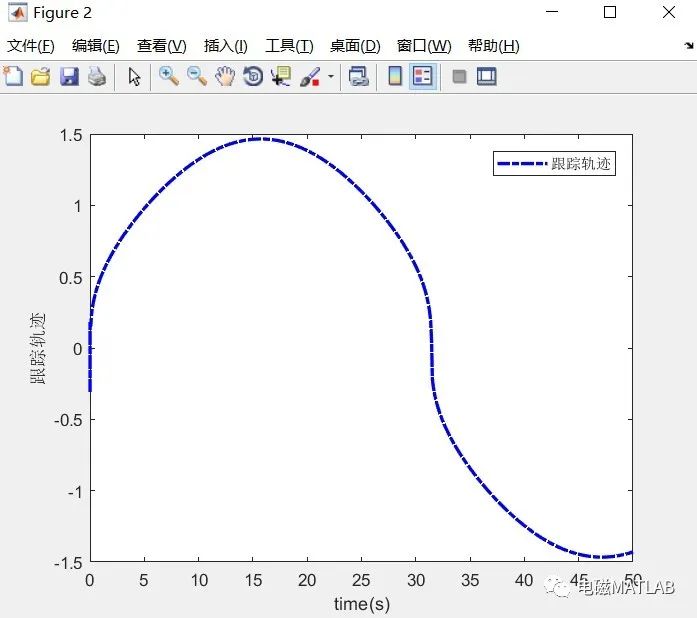
3)轨迹对比
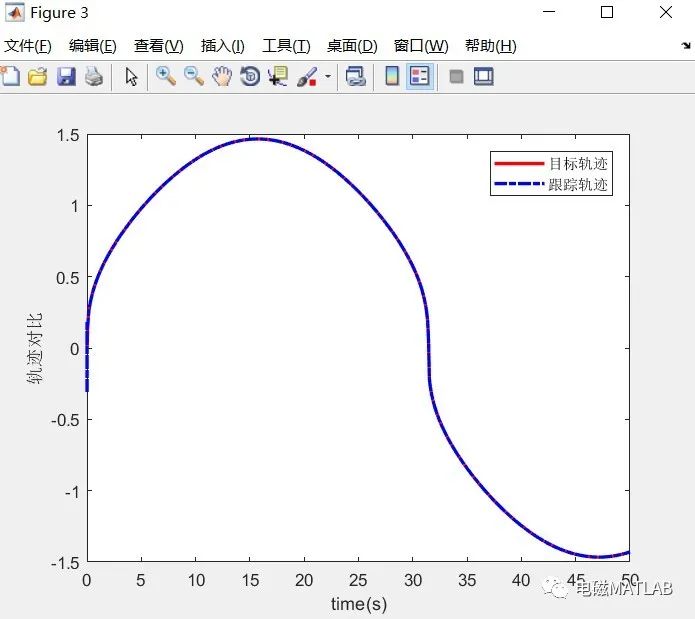
4)跟踪误差
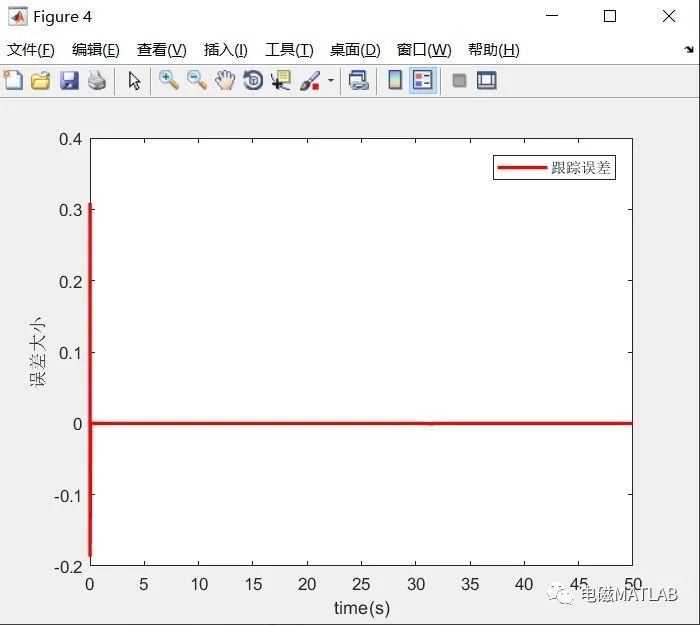
6 matlab程序
%Fuzzy RBF Approximationclear close all;clc%% 参数%学习参数xite=0.50;alfa=0.05;%高斯函数参数bj=1.0;c=[-1 -0.5 0 0.5 1; -1.5 -1 0 1 1.5];%神经网络初始权重w=rands(25,1);w_1=w;w_2=w_1;%输入初始值u_1=0.0;y_1=0.0;%采样时间ts=0.001;%% 轨迹跟踪for k=1:1:50000 %时间time(k)=k*ts;%% 输入层 %输入正弦值 u(k)=sin(0.1*k*ts);y(k)=u(k) y_1/(1 y_1^2);
x=[u(k),y(k)]'; % Layer1:inputf1=x; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 模糊化层for i=1:1:2 % Layer2:fuzzation for j=1:1:5 net2(i,j)=-(f1(i)-c(i,j))^2/bj^2; endendfor i=1:1:2 for j=1:1:5 f2(i,j)=exp(net2(i,j)); endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 模糊推理层for j=1:1:5 % Layer3:fuzzy inference(49 rules) m1(j)=f2(1,j); m2(j)=f2(2,j);end
for i=1:1:5 for j=1:1:5 ff3(i,j)=m2(i)*m1(j); endendf3=[ff3(1,:),ff3(2,:),ff3(3,:),ff3(4,:),ff3(5,:)];%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 输出层f4=w_1'*f3'; % Layer4:outputym(k)=f4; %% 跟踪误差e(k)=y(k)-ym(k);%% 更新学习因子与权重d_w=0*w_1;for j=1:1:25 d_w(j)=xite*e(k)*f3(j);endw=w_1 d_w alfa*(w_1-w_2); u_1=u(k); y_1=y(k); w_2=w_1; w_1=w;end%% 画图输出figure(1);plot(time,y,'r');xlabel('time(s)');ylabel('目标轨迹');legend('目标轨迹');
figure(2);plot(time,ym,'-.b','linewidth',2);xlabel('time(s)');ylabel('跟踪轨迹');legend('跟踪轨迹');
figure(3);plot(time,y,'r',time,ym,'-.b','linewidth',2);xlabel('time(s)');ylabel('轨迹对比');legend('目标轨迹','跟踪轨迹');
figure(4);plot(time,y-ym,'r','linewidth',2);xlabel('time(s)');ylabel('误差大小');legend('跟踪误差');









暂无评论