前面几节我们已经说明白了,在满足一定条件的时候,Buck开关电源可以看成是线性系统,并且可以是划分为4级的反馈控制系统。
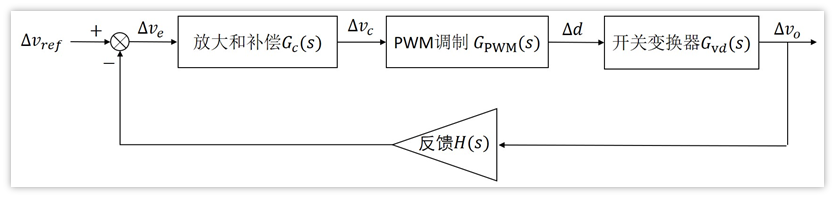
1、反馈级:H(s)
2、放大和补偿级:Gc(s)
3、PWM调制级:Gpwm(s)
4、开关变换级:Gvd(s)
我们要知道整体的传递函数,那么自然需要知道每一级的-传递函数,这一节就先来看反馈级和补偿级的传递函数。
反馈级H(s)和放大补偿级Gc(s)
这两级放到一起说吧,我们分析系统稳不稳定,就要分析开环传递函数T(s)。
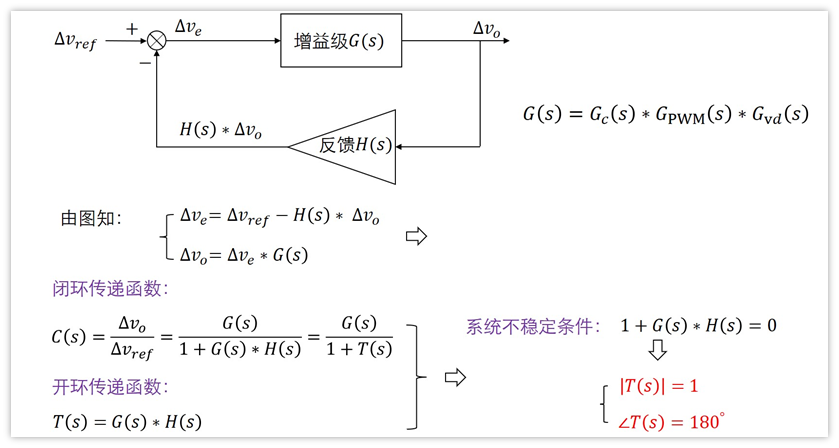
而T(s)等于四级相乘:
T(s)= H(s)*Gc(s)*Gpwm(s)*Gvd(s)
另一方面,反馈和补偿很多时候是揉合在一起的,所以把H(s)和Gc(s)放到一起,求整体H(s)*Gc(s)就可以了,这样更方便计算。
一个问题
Buck我相信每个人都用过,而且应该都会见过下面电路的R3和C3,它们是用作环路补偿的。
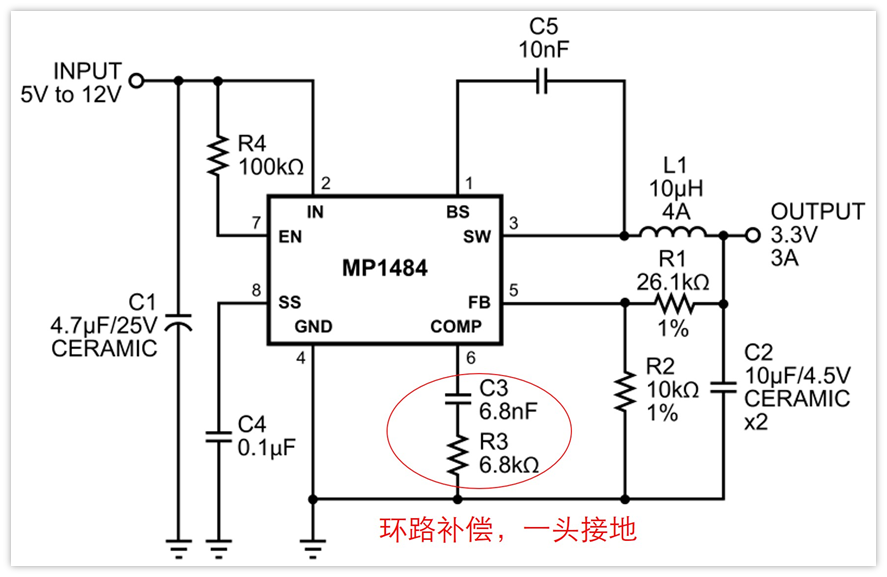
可以看到,上图的补偿电阻和电容的一头都是接地GND的。
另外,我们也会看到一些环路补偿的资料,比如下面的三种补偿。
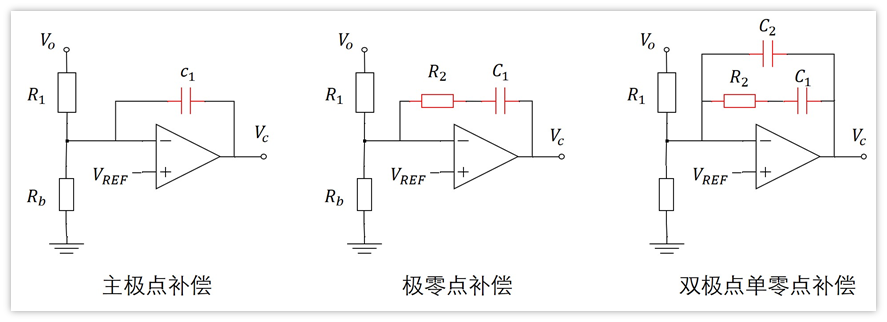
我们发现,这三种补偿,补偿电路都是跨接到输入端和输出端的,并没有接地GND。
这是怎么回事呢?BUCK的补偿电路R和C一头接地,这也能补偿?

这个问题主要是因为误差放大器的不同类型造成的。
误差放大器
我们知道,反馈,放大和补偿,最关键的就是误差放大器,而误差放大器有以下两种:
1、普通放大器
2、跨导放大器
正是因为这两种误差放大器器的不同,所以才导致补偿电路的位置不同。
普通放大器
如下图,是普通的放大器做的放大和补偿:
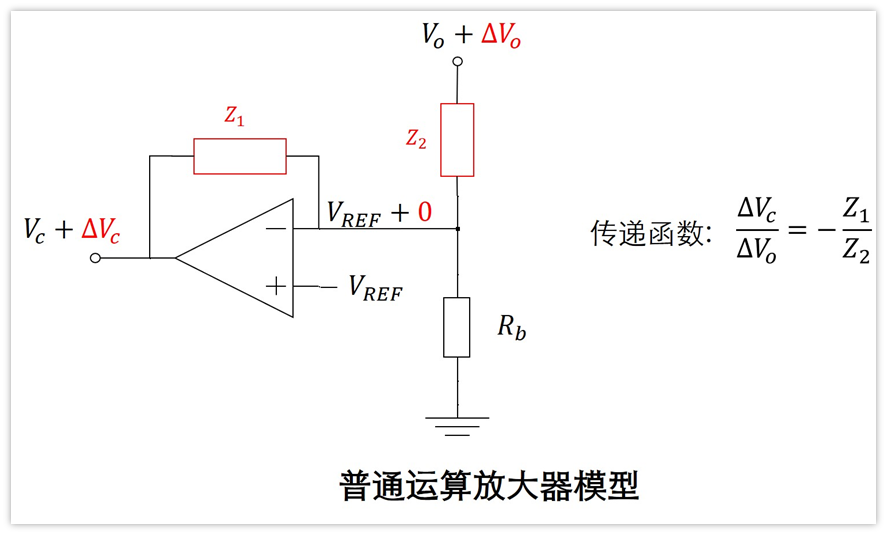
因为电源系统线性化的条件,就有要求是交流小信号,我们只考虑小信号的话,根据放大器的虚短和虚短,就可以求得传递函数。
过程如下:

这个式子能看出什么?
1、分压电阻只有上面那个对环路有影响。
实际电路中,Z2和Rb一般是分压网络的上下两个电阻,可以看到,下面那个电阻Rb对于传递函数没有影响,也就是说它不影响环路稳定性。当然前提条件是误差放大器是普通放大器。
2、实际电路中的Z1
上面的框图我用Z1符号,其实Z1可以由多个器件构成,而我们通常说的三种补偿电路,其实就是Z1的不同。
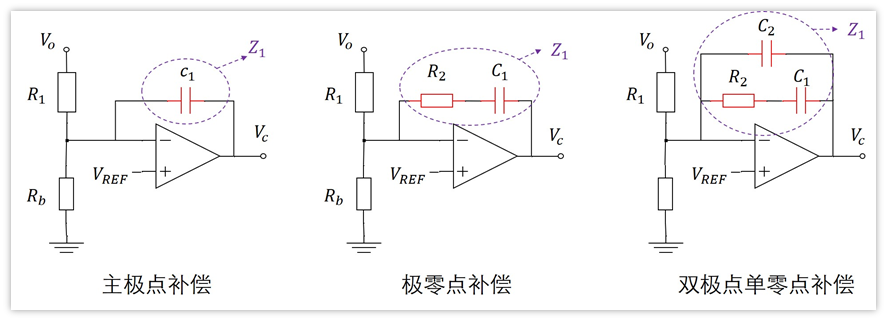
计算方法如下:
主极点补偿:Z1=Zc1
极零点补偿:Z1=Zr2 Zc1
双极点单零点补偿:Z1=Zc2//(Zr2 Zc1)
跨导放大器
普通放大器我们经常用,所以理解起来相对容易,跨导放大器比较陌生一点,但是其实也非常简单。我们先来看下它的定义:
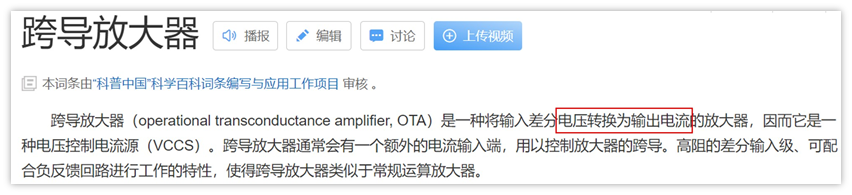
可以看到,跨导放大器最大的特点,就是输入是电压,输出是电流。另外,跨导放大器通常有额外的电流输入端,用以控制放大器的跨导gm。
跨导放大器的输入输出表达式如下:
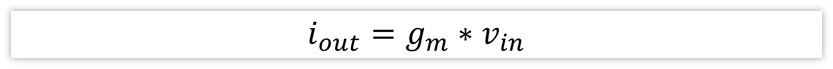
很明显,跨导gm的单位是电流除以电压,也就是A/V,或者是uA/V。其实也有很多其它的单位,比如西门子S,mho,都是一个意思。从量纲上看,A/V=电流/电压=1/电阻Ω=导纳,导纳的单位就是西门子S。
不同厂家的手册,可能会用不同的单位符号表示。
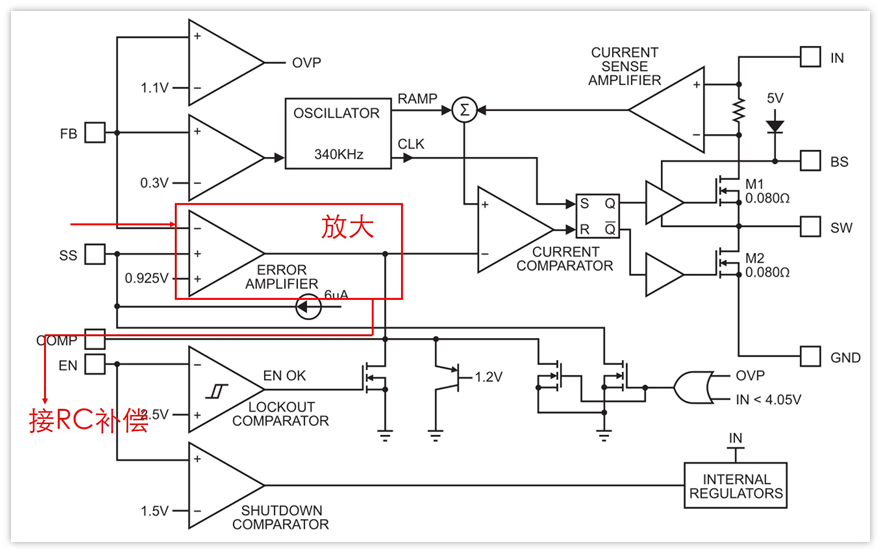
如果大家有注意的话,一些BUCK的手册会把gm这个参数给出来,比如下面BUCK芯片MP1484的参数:

这个Gea应该就是跨导了。
跨导放大器就先这样简单介绍,我们回到主题:误差放大器使用跨导放大器的传递函数是怎么样的?
先看基本电路图:
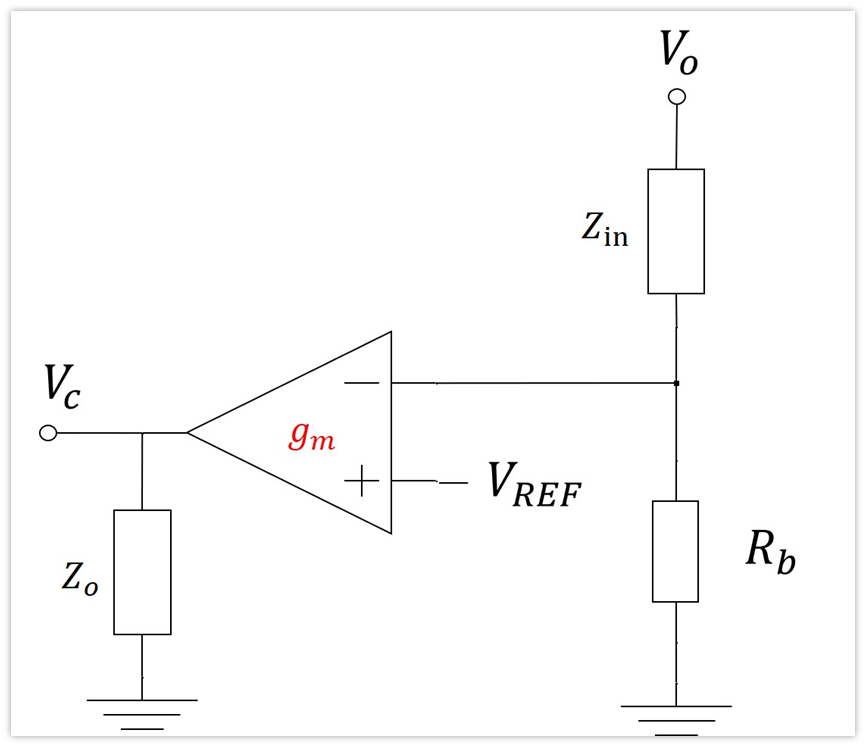
首先需要注意一点,跨导放大器的虚短此时就不成立了,不过其输入阻抗也是很大的(这点值得商榷,这个我查了几个跨导放大器的芯片也并不是很大,有的只有几十K,有的几百K)。
我在一些书上看到,是把跨导放大器的输入阻抗当作无穷大来建模的,所以也就能用“虚断”的概念。不知道是不是开关电源芯片内部的跨导放大器的输入阻抗确实非常大,姑且暂时这么认为吧。
关于跨导放大器,如果想要了解多一点的话,可以看看下面这个文档:
https://wenku.baidu.com/view/cd8b8836b90d6c85ec3ac6a7.html
也可以尝试搜索下CA3080这个跨导放大器芯片,看看它们的参数。
假定跨导放大器的输入阻抗无穷大,那么我们很容易求得上面这个跨导放大器的传递函数。
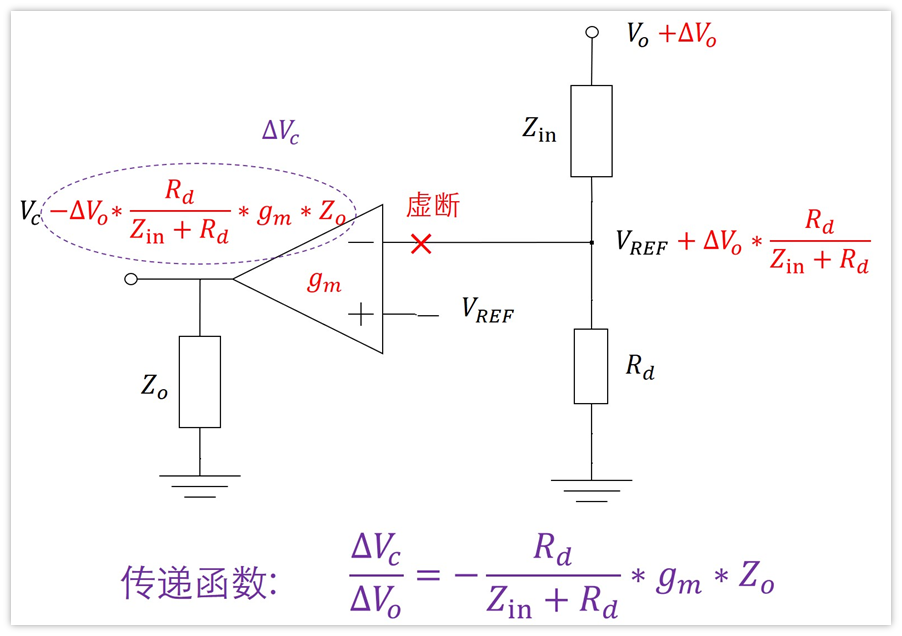
求解过程如下图:

这个式子能看出什么?
1、分压反馈网络的两个电阻对环路都有影响
Zin和Rd分别对应分压反馈网络的上下两个电阻,传递函数有这两个参数,所以两个电阻都对环路有影响
2、实际电路中,补偿电路就是Zo
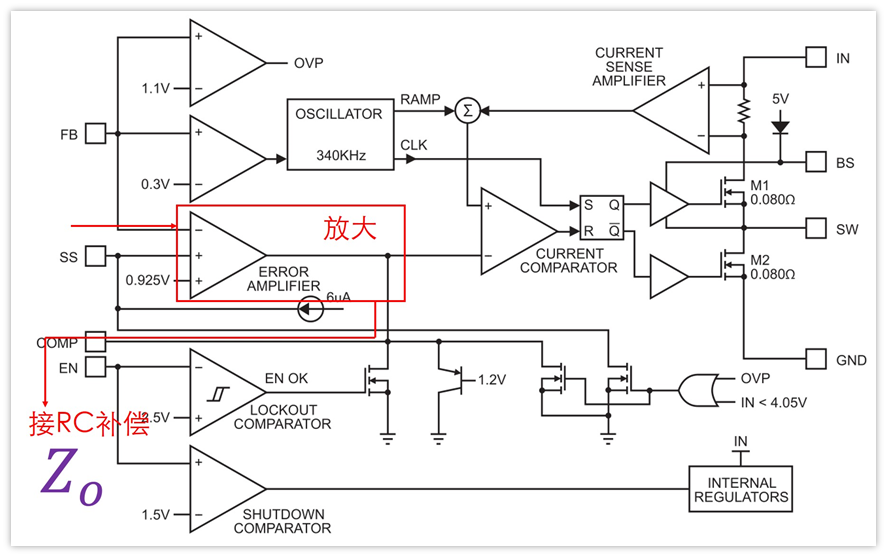
小结
本小节内容介绍了开关电源环路的反馈级和补偿级传递函数,其实主要是对两种不同类型的误差放大器的分析。
主要内容如下:
1、常见的误差放大器有两种形式:普通运放和跨导运放。
2、普通运放的的补偿电路一般跨接在输入和输出,而跨导运放的补偿电路跨接在输出端与GND。
3、不同类型误差放大器,反馈分压电阻的影响不同。普通运放只有上面那个电阻影响环路,而跨导运放,上下两个电阻都会影响环路。
以上内容纯属个人看法,无法保证准确性,建议兄弟们持怀疑的态度去看。如果发现问题也请留言指出来,大家一起进步。









暂无评论