引言
量子计算机在解决某些问题方面大有可为,其速度比经典计算机快得多。然而,构建能够运行商业相关算法的大规模量子计算机仍然是重大挑战。扩展量子计算机的一种方法是采用分布式架构,即将多个量子处理器模块联网。
在本文中将探讨如何利用硅 T 中心作为分布式量子计算的平台。T 中心是硅中的光学活性缺陷,兼具出色的自旋特性和在电信波长范围内发射光子的能力。将 T 中心集成到硅基光电子器件中,并通过光纤将它们连接起来,就有可能创建一个可扩展的模块化量子计算架构。
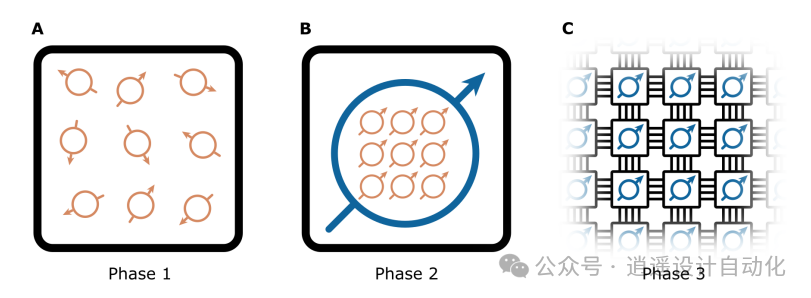 图 1. 量子计算的各个阶段: A. 第一阶段(NISQ)涉及具有噪声物理量子比特(橙色)的单一模块,无法实现 QEC。B. 第二阶段仍然是单模块,但有足够的低噪声物理量子比特来编码逻辑量子比特(蓝色)。C. 第三阶段采用多模块量子计算机,能够容错地实施大规模量子算法。
图 1. 量子计算的各个阶段: A. 第一阶段(NISQ)涉及具有噪声物理量子比特(橙色)的单一模块,无法实现 QEC。B. 第二阶段仍然是单模块,但有足够的低噪声物理量子比特来编码逻辑量子比特(蓝色)。C. 第三阶段采用多模块量子计算机,能够容错地实施大规模量子算法。
T 中心基础知识
T 中心由一个氢原子和硅晶格中的一个碳原子结合而成(图 2A)。T 中心的电子结构包括一个具有电子和核自旋态的基态(GS)和一个具有束缚激子的光激发态(TX0)。在外部磁场的作用下,光学跃迁分裂成两个自旋选择跃迁(标为 B 和 C),可用于自旋初始化、读出和远程纠缠生成(图 3A)。
要创建适合量子计算的 T 中心,需要使用同位素纯化硅来消除不需要的核自旋。然后将 T 中心集成到硅绝缘体(SOI)芯片上的光子空腔中,通过珀塞尔效应增强其光学发射特性(图 3B-C)。
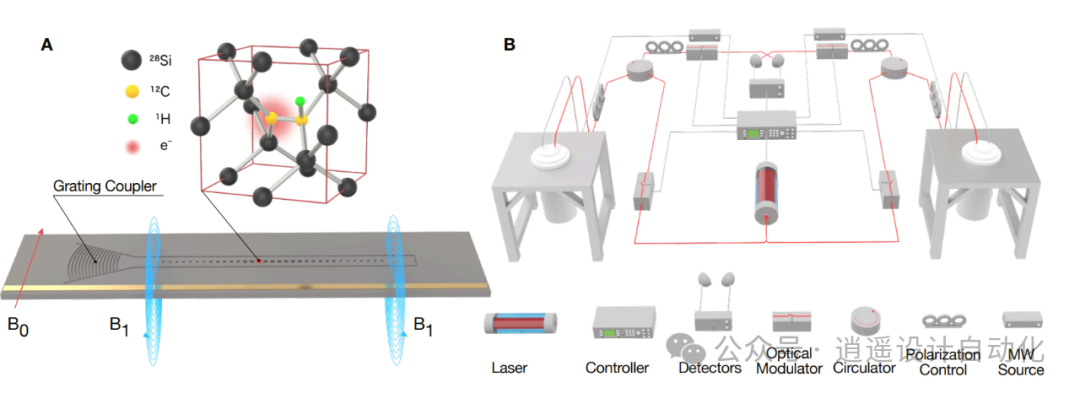 图 2. 演示示意图: A. 光子芯片光腔内硅晶格中的 T 中心,通过光栅耦合器受光激发,自旋跃迁由金属天线的微波和射频驱动。平面内施加磁场 B0,平面外由片上天线产生磁场 B1。B. 两个 T 中心量子比特模块被约 40 米长的光纤隔开,红色为光纤,灰色为电线/微波线。光学调制器包括激发路径上的声光、电光和半导体光学调制器,以及收集路径上的声光调制器。
图 2. 演示示意图: A. 光子芯片光腔内硅晶格中的 T 中心,通过光栅耦合器受光激发,自旋跃迁由金属天线的微波和射频驱动。平面内施加磁场 B0,平面外由片上天线产生磁场 B1。B. 两个 T 中心量子比特模块被约 40 米长的光纤隔开,红色为光纤,灰色为电线/微波线。光学调制器包括激发路径上的声光、电光和半导体光学调制器,以及收集路径上的声光调制器。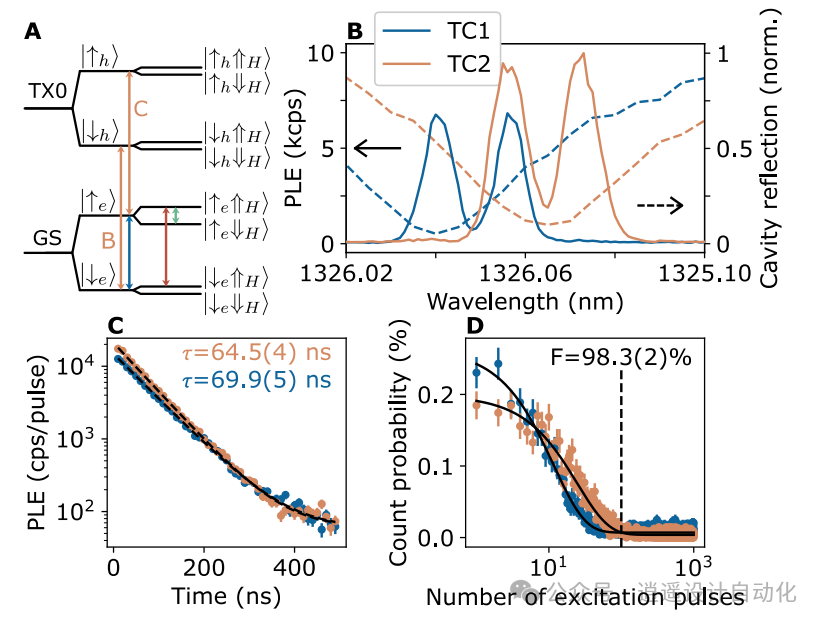 图 3. 单个 T 中心的光学性能: A. 磁场下 T 中心的精细结构,显示电子(|↑e⟩)、激发态空穴(|↑h⟩)和氢(|⇑H⟩)自旋。分裂包括 GS 至 TX0、电子/空穴齐曼分裂以及电子-核超频。B. 磁场为 122.3 mT 时 TC1 和 TC2 的 PLE 光谱,虚线为空腔共振。C. TC1 和 TC2 的 C 和 B 转变的珀塞尔增强寿命。D. 从光泵浦初始化 T 中心,初始化保真度为 98.3(2)%。
图 3. 单个 T 中心的光学性能: A. 磁场下 T 中心的精细结构,显示电子(|↑e⟩)、激发态空穴(|↑h⟩)和氢(|⇑H⟩)自旋。分裂包括 GS 至 TX0、电子/空穴齐曼分裂以及电子-核超频。B. 磁场为 122.3 mT 时 TC1 和 TC2 的 PLE 光谱,虚线为空腔共振。C. TC1 和 TC2 的 C 和 B 转变的珀塞尔增强寿命。D. 从光泵浦初始化 T 中心,初始化保真度为 98.3(2)%。
自旋控制和读出
对 T 中心自旋态的完全控制是通过片上天线发送微波(MW)和射频(RF)脉冲来实现的。电子自旋跃迁由微波脉冲驱动(图 4A-B),而核自旋跃迁则由射频脉冲驱动(图 4C-D)。通过应用适当的脉冲序列,可以实现通用量子门,如受控核自旋跃迁(CNOT)。
核自旋态的单次读出是通过将其映射到电子自旋上进行的,然后通过光学读出(图 4E)。这样就可以对核自旋量子比特进行高保真状态制备和测量(SPAM)。
这项工作中使用的 T 中心显示了超常的自旋相干时间(图 5),电子自旋 T2 时间长达 270 μs,核自旋 T2 时间长达 220 ms。这些长相干时间对于实现高保真量子操作很重要。
 图 4. 单个 T 中心自旋性能: A. ODMR 显示 PLE 信号与两个核自旋选择性 MW 转换频率的 MW 频率。B. 驱动 MW⇓ 核自旋选择性转变的相干拉比振荡,其中 π 旋转构成 CHNOTe 门(插图:基态能级图)。C. 显示核转变共振频率的 ODMR 光谱。D. 相干拉比振荡驱动电子自旋选择性核转变,其中 π 旋转构成 CeNOTH(插图:基态能级图)。E. 核自旋的准备和测量:处于上升或下降状态的核自旋的光子计数(插图:初始化和读出的脉冲序列、状态准备和测量保真度与光子数阈值的关系)。
图 4. 单个 T 中心自旋性能: A. ODMR 显示 PLE 信号与两个核自旋选择性 MW 转换频率的 MW 频率。B. 驱动 MW⇓ 核自旋选择性转变的相干拉比振荡,其中 π 旋转构成 CHNOTe 门(插图:基态能级图)。C. 显示核转变共振频率的 ODMR 光谱。D. 相干拉比振荡驱动电子自旋选择性核转变,其中 π 旋转构成 CeNOTH(插图:基态能级图)。E. 核自旋的准备和测量:处于上升或下降状态的核自旋的光子计数(插图:初始化和读出的脉冲序列、状态准备和测量保真度与光子数阈值的关系)。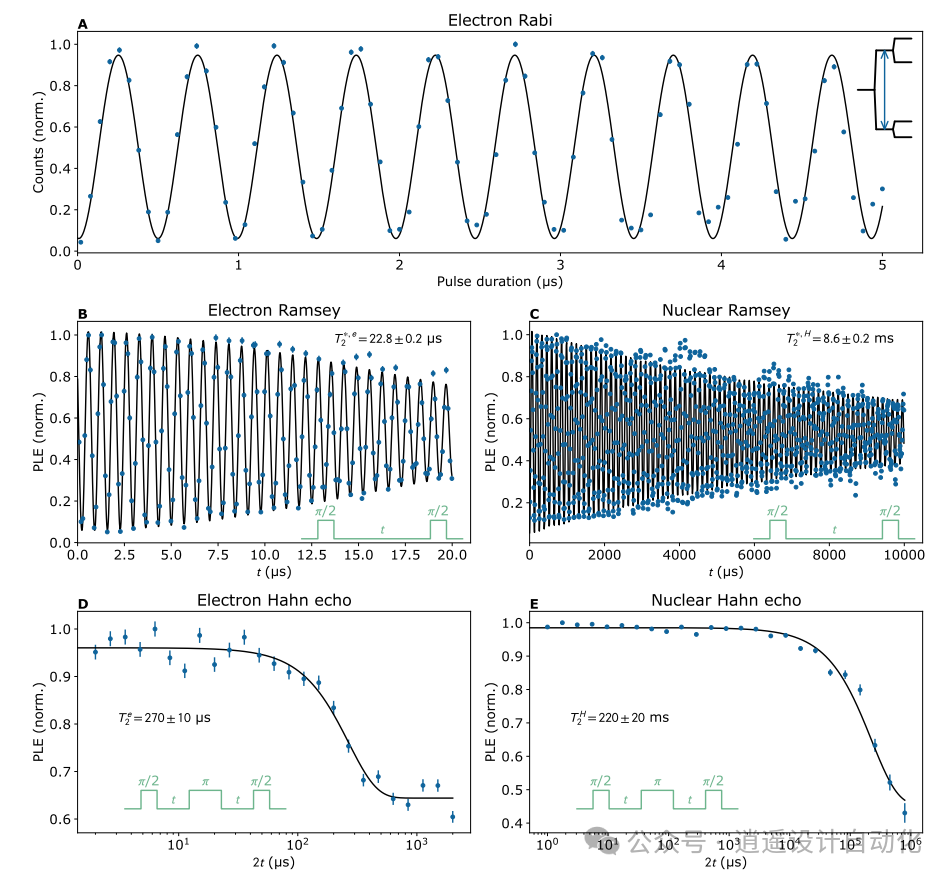 图 5. 自旋相干时间 A. 无核选择性的电子拉比振荡(插图:驱动转换)。B、C. 拉姆齐干涉条纹显示电子和核自旋的 T∗2 衰变(插图:脉冲序列)。D、E. 电子自旋和核自旋的哈恩回波 T2 衰减曲线(插图:脉冲序列)。材料和制造工艺的改进可显著提高器件集成 T 中心的相干时间,接近在块体 28Si 中观察到的相干时间(核自旋为 0.28 秒,电子自旋为 2.1 毫秒)。
图 5. 自旋相干时间 A. 无核选择性的电子拉比振荡(插图:驱动转换)。B、C. 拉姆齐干涉条纹显示电子和核自旋的 T∗2 衰变(插图:脉冲序列)。D、E. 电子自旋和核自旋的哈恩回波 T2 衰减曲线(插图:脉冲序列)。材料和制造工艺的改进可显著提高器件集成 T 中心的相干时间,接近在块体 28Si 中观察到的相干时间(核自旋为 0.28 秒,电子自旋为 2.1 毫秒)。
远程纠缠
要实现分布式量子计算,必须在不同芯片上的 T 中心之间建立远程纠缠。这可以通过一种称为巴雷特-科克(BK)的协议来实现(图 7A),该协议依赖于 T 中心发射的光子的干涉。
成功产生纠缠的关键要求是所发射光子的不可分性。这可以通过洪欧-曼德尔(HOM)能见度(图 6)来量化,它可以测量来自不同 T 中心的光子之间的量子干涉程度。通过优化 T 中心的光谱和时间特性,可以实现高可见度的 HOM 干涉。
利用 BK 协议,T 中心电子自旋的远程纠缠得到了证实,保真度高达 60%(图 7B)。产生的纠缠随后被用于在远程 T 中心的核自旋量子位之间执行远程传输 CNOT 门(图 8-9),展示了分布式量子逻辑的潜力。
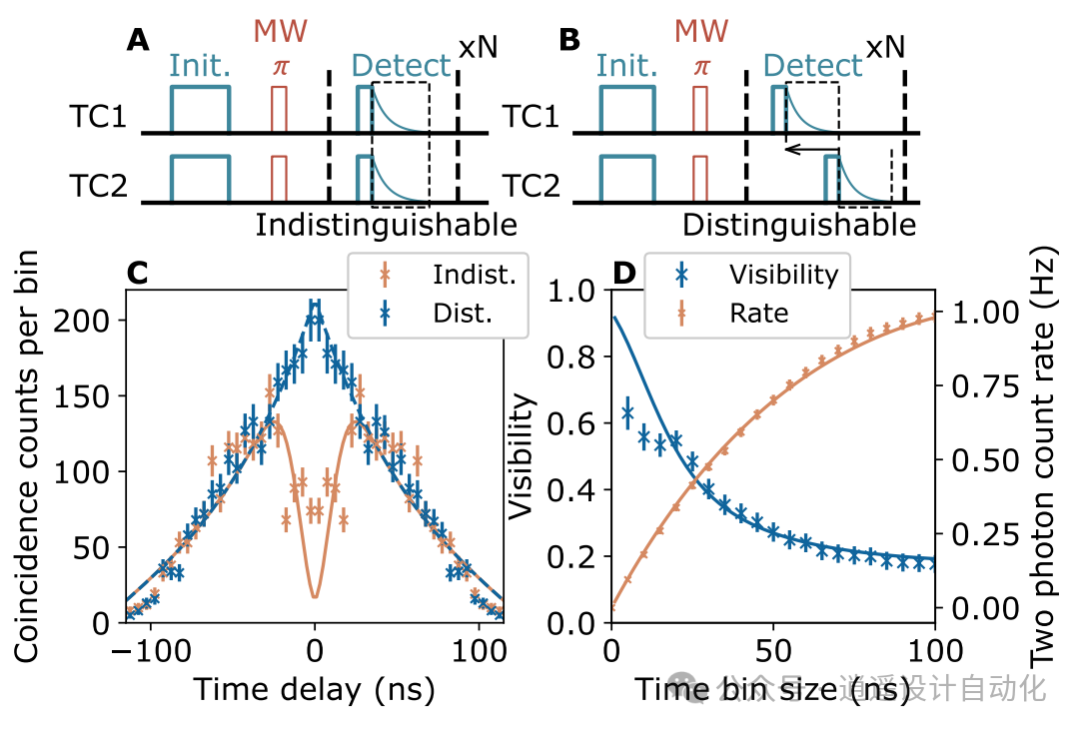 图 6. 虹欧-曼德尔双光子干涉: A. 收集不可分事件的脉冲序列。B. 收集可区分事件的脉冲序列。在分析中,TC2 的延迟光脉冲的时间标记被移位,以便与 TC1 的第一次光激发和检测相一致。C. 测量到的可分辨事件(橙色十字)和不可分辨事件(蓝色十字)的重合计数与泊松误差,并与模型重叠(蓝色实线和橙色虚线)。D. 双光子可见度与时间滤波器大小(蓝叉)和模型(蓝色虚线)的函数关系,以及可分辨重合计数率与泊松误差和模型(橙色实线)滤波(橙叉)的函数关系。
图 6. 虹欧-曼德尔双光子干涉: A. 收集不可分事件的脉冲序列。B. 收集可区分事件的脉冲序列。在分析中,TC2 的延迟光脉冲的时间标记被移位,以便与 TC1 的第一次光激发和检测相一致。C. 测量到的可分辨事件(橙色十字)和不可分辨事件(蓝色十字)的重合计数与泊松误差,并与模型重叠(蓝色实线和橙色虚线)。D. 双光子可见度与时间滤波器大小(蓝叉)和模型(蓝色虚线)的函数关系,以及可分辨重合计数率与泊松误差和模型(橙色实线)滤波(橙叉)的函数关系。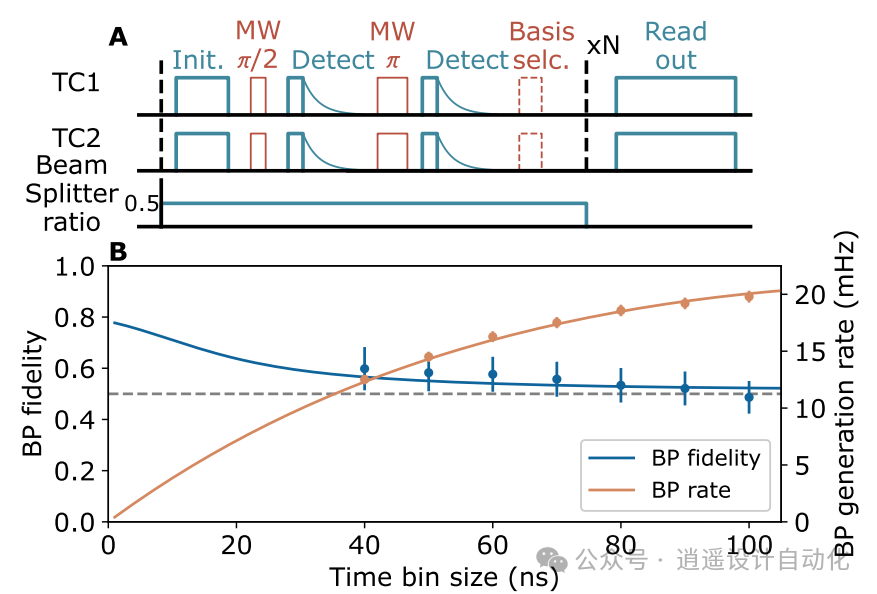 图 7. Barrett-Kok 方案演示: A.BP纠缠脉冲序列,光泵浦初始化,然后是纠缠序列。最后的微波脉冲决定了读出的基础。B. 不同时间间隔大小的 BP 生成率和保真度。
图 7. Barrett-Kok 方案演示: A.BP纠缠脉冲序列,光泵浦初始化,然后是纠缠序列。最后的微波脉冲决定了读出的基础。B. 不同时间间隔大小的 BP 生成率和保真度。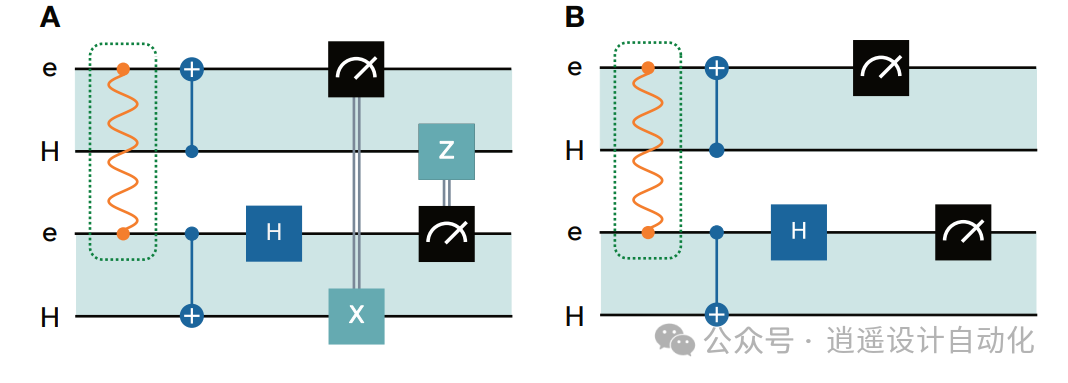 图 8. 远传 CNOT 电路图: A. 不同模块 T 中心氢原子核(H)之间的 tCNOT,突出显示同一 T 中心电子(e)与原子核之间的空间。首先,在电子上建立分布式贝尔对,然后实施本地测量和操作,完成 tCNOT。B. 后选远程传输 CNOT 电路,通过省略前馈操作和后选测量结果 00 来实现。
图 8. 远传 CNOT 电路图: A. 不同模块 T 中心氢原子核(H)之间的 tCNOT,突出显示同一 T 中心电子(e)与原子核之间的空间。首先,在电子上建立分布式贝尔对,然后实施本地测量和操作,完成 tCNOT。B. 后选远程传输 CNOT 电路,通过省略前馈操作和后选测量结果 00 来实现。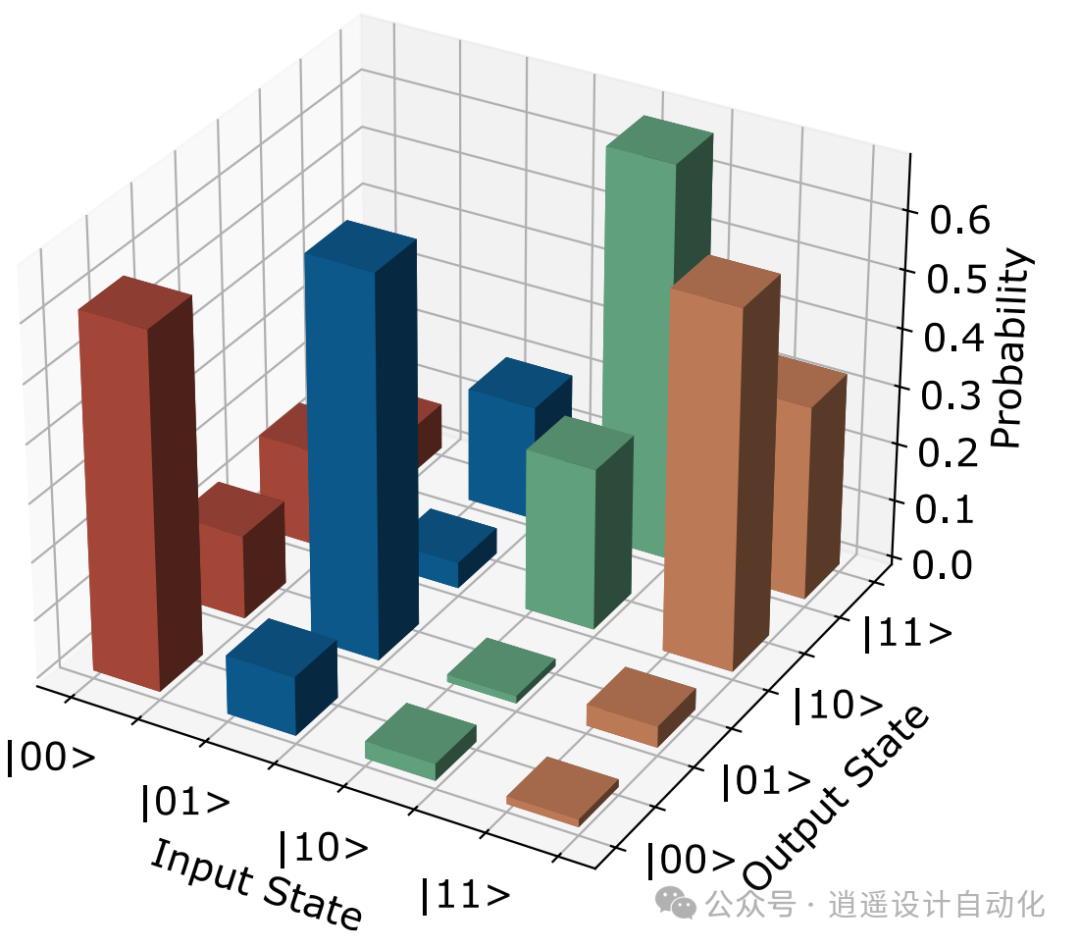 图 9. 初步 T 中心遥传 CNOT 序列的真值表: 使用后选 CNOT 的初始 tCNOT 实验真值表。
图 9. 初步 T 中心遥传 CNOT 序列的真值表: 使用后选 CNOT 的初始 tCNOT 实验真值表。
展望与结论
根据实验结果和 T 中心器件的预期改进,预计可以实现高达 99.9% 的远程纠缠保真度和 200 kHz 的分布率(图 10)。这将实现跨多个 T 中心处理器模块的容错分布式量子计算。
硅 T 中心为实现分布式量子计算机提供了一个前景广阔的平台。利用成熟的硅光子产业和 T 中心的优异特性,也许有可能建立模块化、可扩展的量子计算系统,从而解决商业相关问题。本文中介绍的成果是实现这一目标的重要第一步,推进未来分布式量子计算技术的进步。
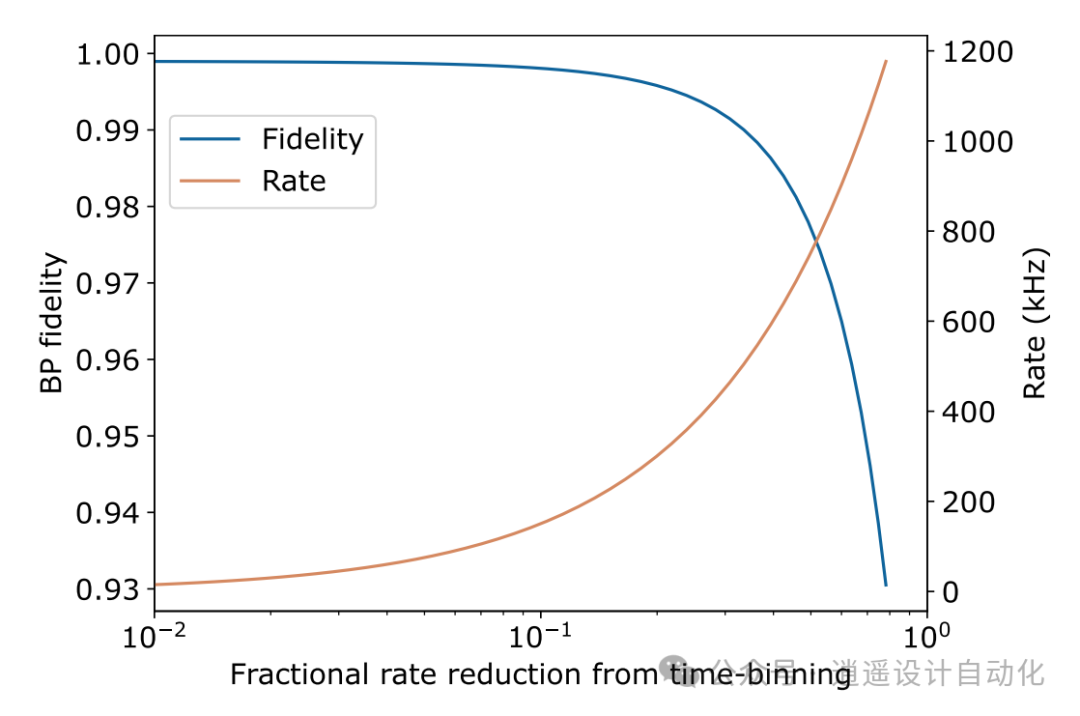 图 10. 使用预测 T 中心性能的远程贝尔对分布的保真度和速率: 时间窗相关滤波器增强了纠缠保真度,并捕捉到了一部分重合。还考虑了其他不保真来源,如双重激发和非共振激发。
图 10. 使用预测 T 中心性能的远程贝尔对分布的保真度和速率: 时间窗相关滤波器增强了纠缠保真度,并捕捉到了一部分重合。还考虑了其他不保真来源,如双重激发和非共振激发。











暂无评论