“时间常数”哪学来的？

     “电路”/“信号与系统”/“自动控制原理”，多次揭示一阶系统的运行规律，其中τ(tao)就是时间常数time constant。电路中，RC串联的零状态响应是典型的一阶电路，τ=RC。

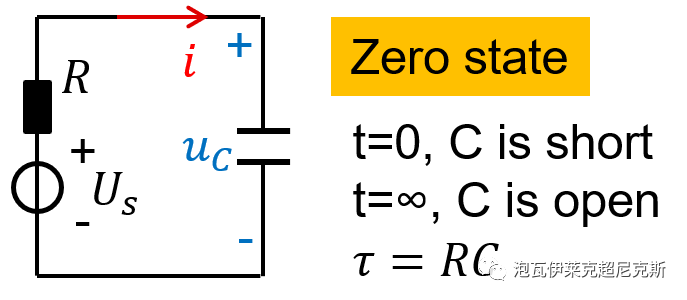
    若u(t)为单位阶跃输入，输出y(t)经过3-5个τ的滞后才可近似认为进入了稳态，达到静态增益k。

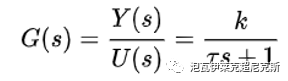
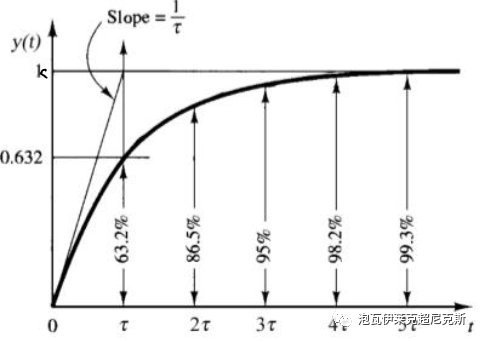
    简言之，“时间常数”只针对一阶系统，广义上的时间常数或可针对主导极点为一阶形式的，类一阶的高阶系统。直观地说，它代表了系统对抗外界变化，保持原状的抵抗能力（惯性）。

    那么，从稳态来看，只要我身为舔狗等女神足够久，一阶环节的时间常数并不会对直流输入产生影响。

直流书上都有，交流呢？

    实际工程的采样环节中，除了直流信号，我们常遇到交流信号（或含交流信号）的调理与高频噪声滤除，最简单且典型的，即采用一阶滤波电路实现。

    滤掉高频噪声很简单，但我们也应该关心，经过时间常数τ的一阶滤波，正弦输入基波的稳态响应，有没有可能被滤过头？

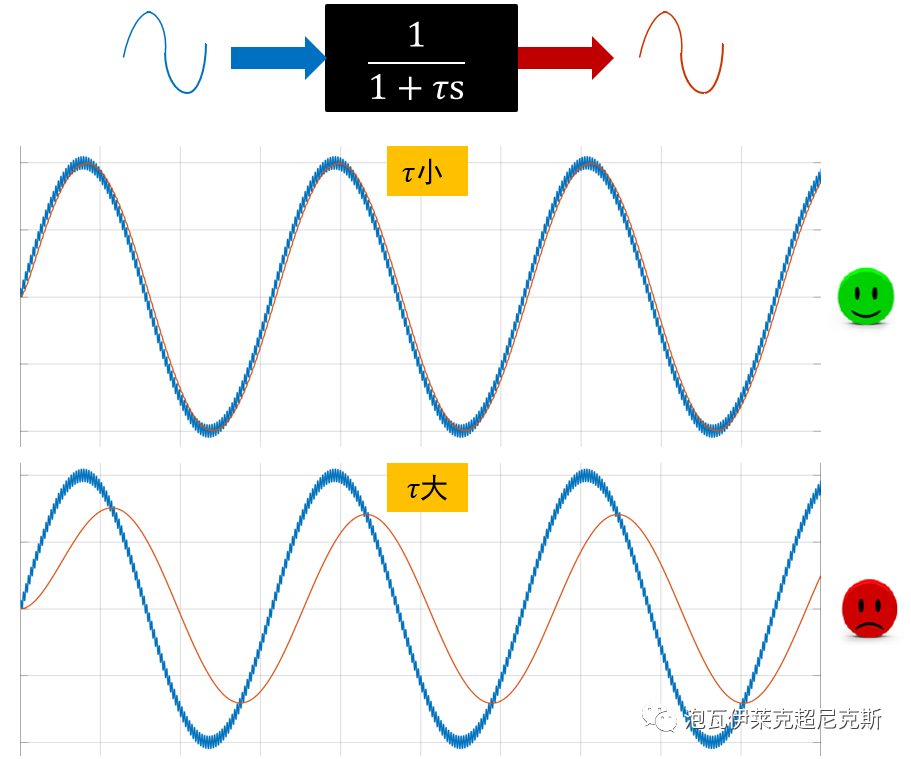
    从用户友好 小白实用的角度出发，必然是直接从时域得到结论。

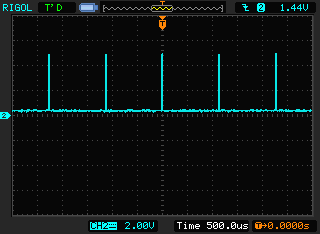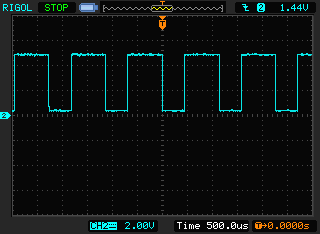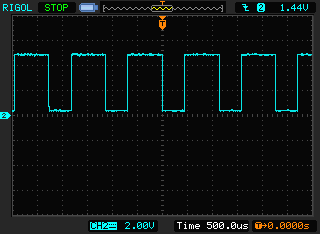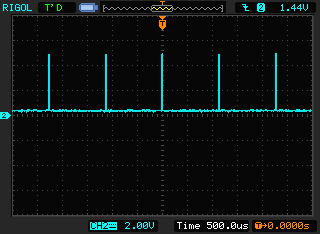
•   已知输入波形周期100us，一阶滤波器的时间常数取多少us才可以不失真（幅度，相位）？

•   系统稳定后，输入输出两个正弦的基波，在时域上有多少延迟？

  
  

    不必每次都理论计算/仿真，而能秒答这两个问题，加速调试和设计过程，是本文撰写的初衷。

怎么分析？

    为了尽可能量化，联系理论工具：正弦稳态响应→波特图。

    一阶系统波特图和渐近线如下，转折频率为蓝色线fc，输入的ac信号基波频率为绿色线fac。

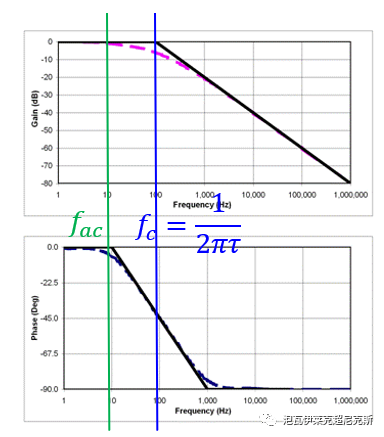
    由图可知，为了几乎不产生衰减和相移的失真，放在转折频率1/10以下，fac

    我们就把fac放在fc/10的地方，为了找出时间常数和交流信号，在时域的直接关系，列表如下：

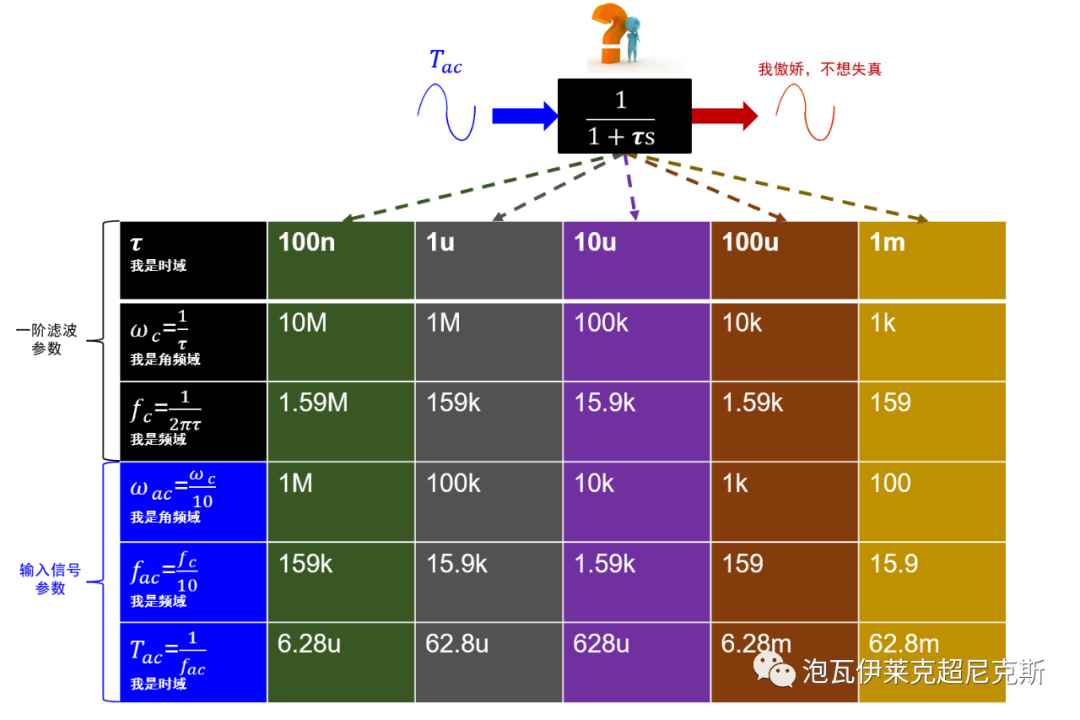
     结论：频域幅度和相位的不失真，即时域上幅度缩小和时间延迟近似忽略的情况下，在时域上需求的倍数关系高达62.8，也就是说，针对100us周期的输入信号，滤波器时间常数不要超过1.6us。

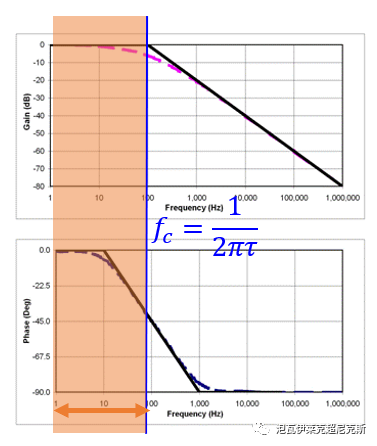
    那么，为了研究时域延迟，如果让输入信号频率fac在fc之下自由移动，（上图中橙色区域），即周期低于20pi*τ，相移会有负的0°-45°之多，对应的时域呢？

    一阶系统相位表达式如下，橙色区域恰对应自变量2pi*f*τ的范围在[0，1]。

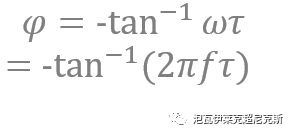
    百度一下，白嫖个函数图像：

    为了避免用大一高等数学的泰勒展开和各阶近似把人绕晕，直接由图可知：

x→0（无穷小），有y=-x成立；x=1时，y=-x*pi/4。

    如果你愿意，可以把这段区域用y=-x和y=-x*pi/4包起来。

    因此，知道了相角，由高中数学三角函数知识，显然可以得到对应的时间：

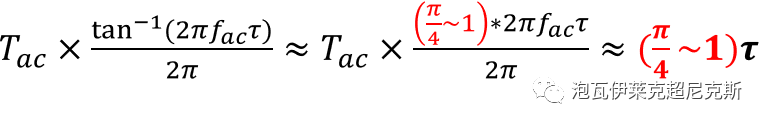
    结论：近似的，通过时间常数为τ的一阶系统，若输入的交流信号频率处于相对中低频（低于转折频率fc），输出产生的延迟约在0.785τ~τ之间。

总结下

    这就是大家的直觉印象，交流信号通过时间常数τ的滤波器，会产生大约τ的时域延迟的由来。

    但要注意，该结论的近似条件，只到转折频率fc，也就是低频才可等效。

    某种程度上，这也直接从时域等效的角度，解释了耳熟能详的：在相对低频段，τ的纯延迟环节可以和时间常数τ的一阶惯性环节，相互近似等效。

    如果从频域的角度，画出延迟环节（含e的超越函数）的波特图曲线，可以发现在低频段，其相角和一阶系统差异很小。

    究其数学根本，就是高数的泰勒展开近似。感兴趣的同学可以自行查阅陈伯时老师的“电力拖动自动控制系统”课本，附录中针对该近似的推导。