香农采样定理，也叫做奈奎斯特采样定理，是信息论与信号处理领域中的一个核心定理。它确立了连续时间信号（模拟信号）与离散时间信号（数字信号）之间的转换关系，为数字信号处理及通信技术的发展奠定了理论基础。

1、香农采样定理是什么？

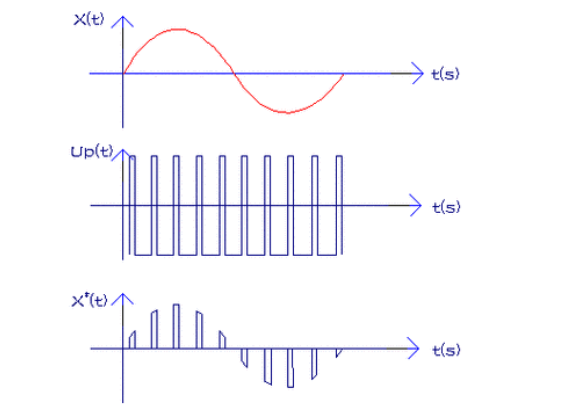
香浓采样定理指出，如果一个连续时间信号是带限的，即其频谱分量中频率高于某一特定值（称为带宽）的部分为零，那么这个信号就可以通过等间隔采样来完全恢复。采样的频率必须大于等于信号最高频率的两倍，这一最小的采样频率被称为奈奎斯特频率。

2、香农采样定理相关公式

①基本公式：

f_s \geq 2f_{max} \] 其中，\(f_s\) 是采样频率，\(f_{max}\) 是信号的最高频率。这一公式直接给出了采样频率与信号最高频率之间的最小关系。

②理想低通信道最高码元传输速率公式（虽非直接由香浓提出，但相关）：

B = 2W \] 其中，\(B\) 是理想低通信道的最高大码元传输速率，\(W\) 是信道的带宽。这一公式由奈奎斯特在1924年推导，与香浓采样定理在理论上有紧密联系。

③信息传输速率公式（同样非直接由香浓提出，但相关）：

C = B \cdot \log_2 N \] 其中，\(C\) 是信息传输速率，\(B\) 是带宽，\(N\) 是电平强度。这一公式进一步说明了在给定带宽下，信息传输速率与电平强度的关系。

本文凡亿教育原创文章，转载请注明来源！