本节我们讲一些无刷电机FOC矢量控制的入门知识。
1)FOC矢量控制的作用我们前两节讲的无刷电机(BLDC),是最简单的一种结构,当转子匀速转动时,定子内产生的反电动势是梯形波;在驱动无刷电机转动时,线圈中只有加电和不加电两种状态,所以转矩是脉冲式的,转动的过程不平稳,会有顿挫感。虽然增加电机的极对数可以减轻这种不平稳特性,但是极对数不能无限增加。
FOC矢量控制,就是研究怎样控制无刷电机的几个定子线圈中的电压,使得它们产生的磁场效果之和,能产生稳定的转矩,使转子平稳地转动。为了达到这一目的,需要使用一种特殊的无刷电机——永磁同步电机。
永磁同步电机(PMSM)的转子和定子间的磁路是经过特殊设计的,使得转子转动时,定子内的反电动势是正弦波;在驱动它时,也使用正弦电压驱动,那么它的转矩大小就有可能保持不变,使得转动更加平稳。通常我们所说的FOC矢量控制,都是指的用三相正弦电压去驱动永磁同步电机。
另外,普通的梯形波反电动势的无刷电机也可以用FOC矢量控制驱动。因为梯形波可以近似为正弦波,所以使用永磁无刷电机的正弦波矢量控制法,也是可以驱动普通的梯形波无刷电机的,只是相比永磁同步电机转矩的稳定性稍差。
2)FOC矢量控制的实现方法由于FOC矢量控制的目的是要能实现一个大小固定,方向旋转的转矩。如下图所示,也就是定子产生的磁场之和要大小固定,方向稳定地旋转:
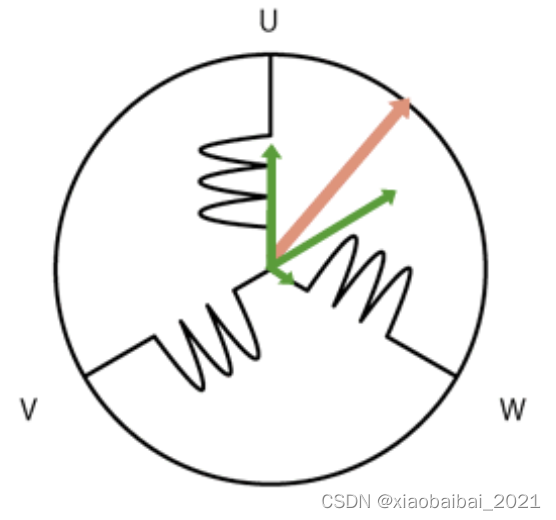
不难想到,当三相线圈中通过幅度相同、相位相差120°的正弦波电流时,可以得到一个旋转的磁场,而且这个磁场的大小是恒定的。而这个三相正弦波,需要与转子的位置、转速相匹配,才能把电机顺利驱动起来。具体来说,正弦波的相位与转子位置相关,正弦波的幅值与转速(电压控制电流,电流控制转矩)相关。
FOC矢量控制,就是要依据转子的位置和转速,来确定一个合适的三相正弦波电压去驱动定子线圈。但是,直接通过转速和位置去推算三相电的特性比较困难,我们需要使用各种数学变换来降低控制的难度。
a)基础的数学变换我们先来熟悉一下几个数学变换,之后再讲如何使用它们去实现FOC控制。
Clarke变换
Clarke也叫3s/2s变换,是一个实现三相到两相的变换。
在三相线圈中,通过的电流Ia、Ib、Ic,它们产生的电流矢量在平面上,是可以变换到一个直角坐标系中的,这样,可以把三相变换为两相,如下图:
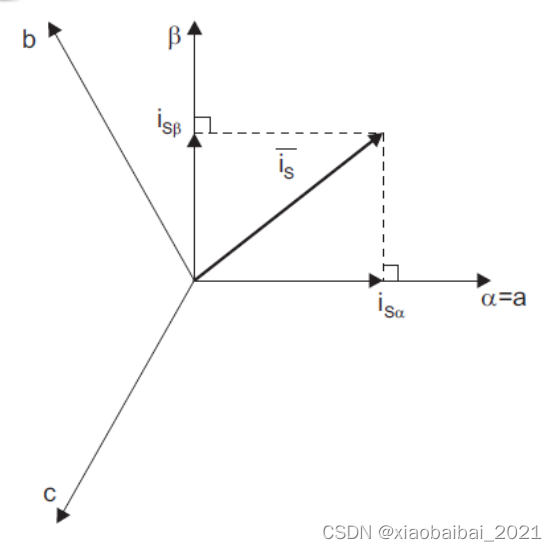
a、b、c坐标系里的电流之和,可以通过以下公式变换到α、β直角坐标系中:
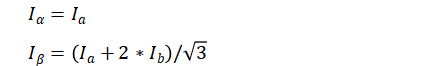
这样,我们就把相差120°的三相电流,变换成了正交的两相电流。
Park变换
Park又叫2s/2r变换,是一个实现两相静止到两相旋转的变换。
如下图,α、β是一个静止的直角坐标系,d、q是一个绕原点旋转的直角坐标系(与转子相对静止,d方向的电流矢量能产生转矩,q方向的电流矢量不能产生转矩):
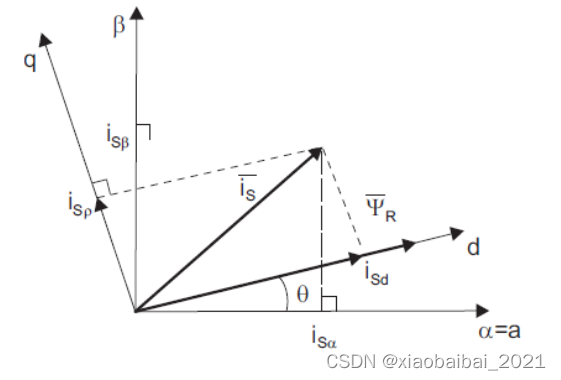
α、β坐标系里的电流之和,可以通过以下公式变换到旋转的d、q直角坐标系中:
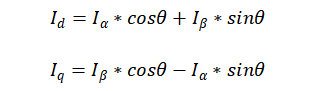
同样地,不难得出Park逆变换,把旋转的d、q直角坐标系中的矢量,变换为静止的α、β坐标系中的矢量可以使用如下公式:
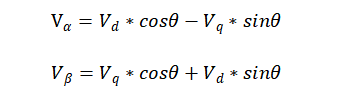
好了,讲了几个变换的,那么对于简化FOC的实现有什么作用呢?我们把三相的电流Ia、Ib、Ic经过Clarke变换,再经过Park变换,会发现,旋转的电流矢量,转换到旋转的d、q坐标系以后,变成了两个固定的电流Id和Iq。
通过这两层变换之后,我们再来控制电流矢量的大小就简单得多了,而控制了电流就等于控制了转矩。
下面这张图是FOC矢量控制的基本框图:
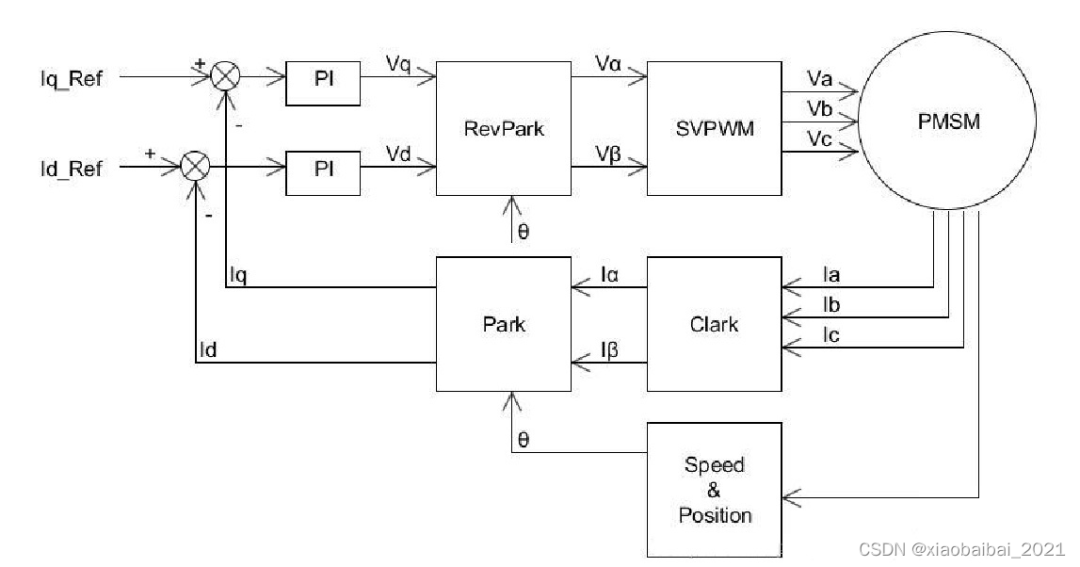
FOC控制的步骤如下:
(1)采集无刷电机的三相电流Ia、Ib、Ic;
(2)进行Clarke变换,计算出电流Iα、Iβ;
(3)进行Park变换,计算出电流Iq、Id(这一步需要用到转子的角度信息);
(4)依据特定的控制策略,来调节Iq、Id的大小,图中使用的是PID控制(只用了PI);
(5)PID控制器的输出,是电压Vq、Vd(旋转坐标系下的电压),因为控制电压也就控制了通过电机的电流;
(6)再通过Park反变换,把Vq和Vd变换为静止的直角坐标系下的Vα、Vβ(这一步也需要转子角度信息);
(7)最后用SVPWM方法来实现Vα、Vβ的输出,驱动三相全桥;
我们经过clarke变换、park变换,把电流三相交流电变换到了一个虚拟的坐标系下,变成了两个直流电,是为了方便控制;得到了虚拟的控制量之后,还要反变换回去,得到三相电的控制量。
注意上面步骤中这个“特定的控制策略”,一种最容易想到的方法是使得Id=0,控制Iq的大小去控制转矩,这样效率最高,也是最常见的一种FOC控制方法。
除了Id = 0策略,还有多种控制策略,如:单位电流电磁转矩最大控制、弱磁控制、最大输出功率控制,等等多种控制方法,有兴趣可以自行钻研。
c)SVPWM实现FOC的基本框图中,SVPWM是控制中重要的一步,它把Vα、Vβ两相正交的电压矢量变换成了三相全桥的控制量。它是如何工作的呢?
如下图的三相全桥,每个桥臂同一时刻上、下管只能导通一个:
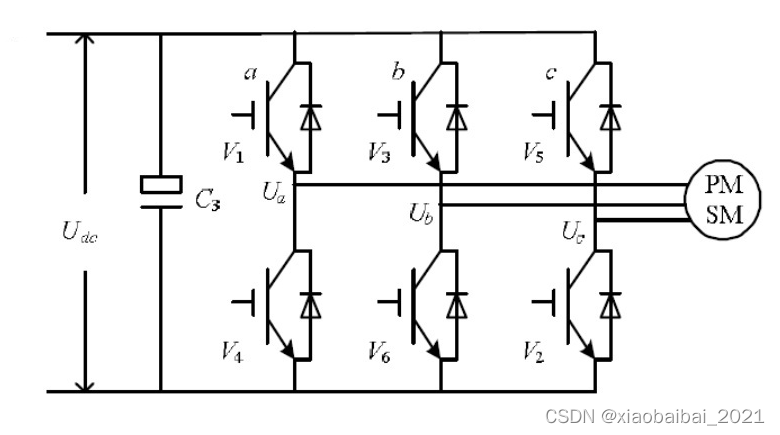
我们将上管导通记为1,下管导通记为0,那么各种导通情况下共有8种导通组合,可产生的电压矢量U0~U7如下图所示:
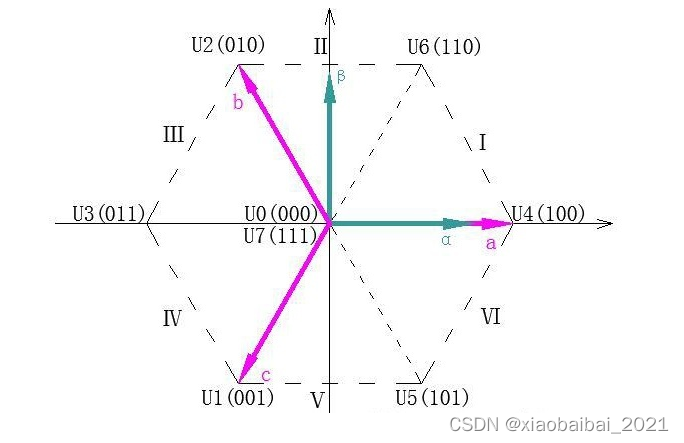
除去000和111两种电压矢量为0的情况,可以输出U1~U6六种电压矢量。这六个电压矢量把平面分成了六个区,平面内的任一电压矢量,都可以通过它所处区间两边的两个电压矢量来合成。
具体来说,可以分为两步:先确定在哪个扇区,再确定各矢量的大小。如下图:
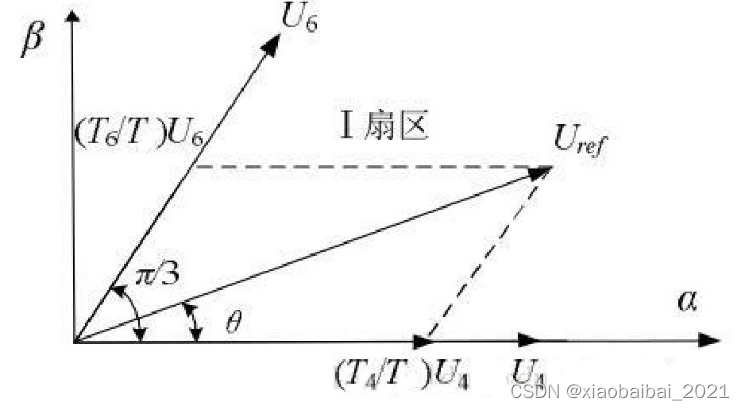
假定要产生的电压矢量为Uref,Vα、Vβ是两个正交轴上的投影,首先可以通过Vα、Vβ的正负以及大小确定Uref处于哪个扇区。
如上图,若处于U4和U6之间,那么就可以用U4和U6两个矢量来合成Uref矢量。
我们可以通过角度θ,来计算Uref在U4和U6两个方向上投影的比例大小,再依据这个比例,去设置一个周期T之内输出U4和U6电压矢量的时间,就能保证输出的矢量方向与Uref相同;同时,使用PWM脉宽调制来控制电压的大小。这样,我们就可以通过U4和U6来合成Uref电压矢量了。
假如U4导通时间为T4,U6导通时间为T6,则T4和T6的比例大小如下(T为一个控制周期,m是SVPWM的调制系数,m=√3*Uref/Udc):
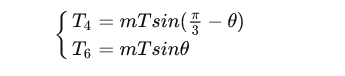
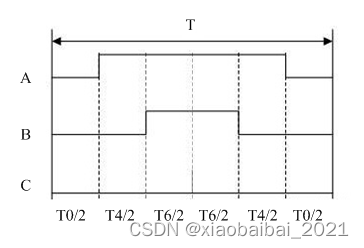
一种划分各段时间的方法是,在一个周期中,把时间分成如下几个片段(实际切换7次状态,通常称为7段式):
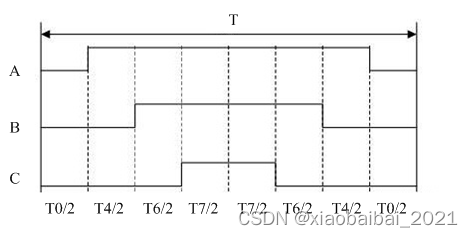
在T0时桥臂导通000,T4时间导通100,T6时间导通110,T7时间导通111,这样在一整个周期中,通过控制T4和T6时间的大小,可以控制合成电压矢量的方向,通过控制PWM波的占空比可以控制合成电压矢量的大小,我们的输出就与Uref一致了。
另外,注意T0时间段和T7时间段,都是输出0矢量。在非零矢量中间插入零矢量的输出,主要是为了降低谐波分量。选择000矢量还是111矢量,要看合成电压在哪个扇区,哪一种切换的状态变化最少。
除了上面的7段式,也有5段式控制,如下图所示:
上面已经把FOC最基本的几个模块讲完了,但是只讲了如何控制电机的电流,使得电机平稳转动。实际上,在电机的控制系统中,我们还希望能控制电机的转速、位置等等。
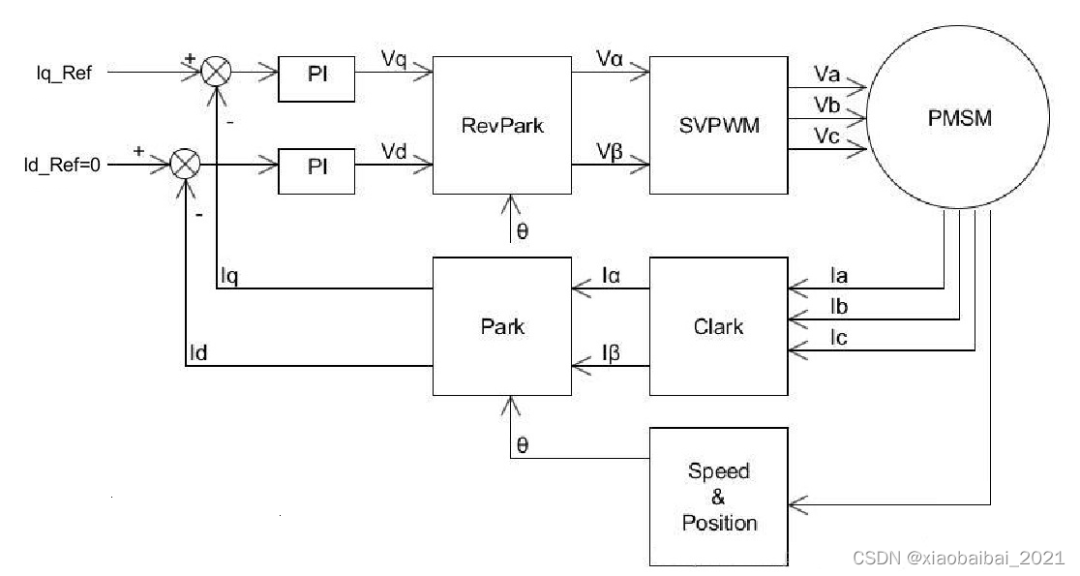
在b)节中出现的FOC基本的框图,只控制了电流,并没有对电机的转速、位置进行控制,所以称为电流环控制:
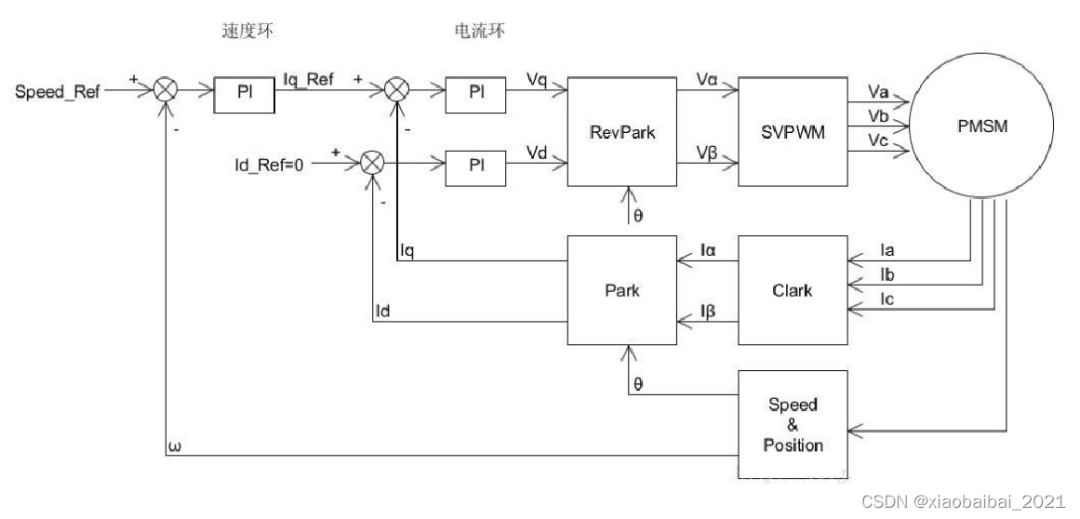
当我们在上述系统中,增加转速控制的PI环节后,变成了如下框图形式,双环控制:
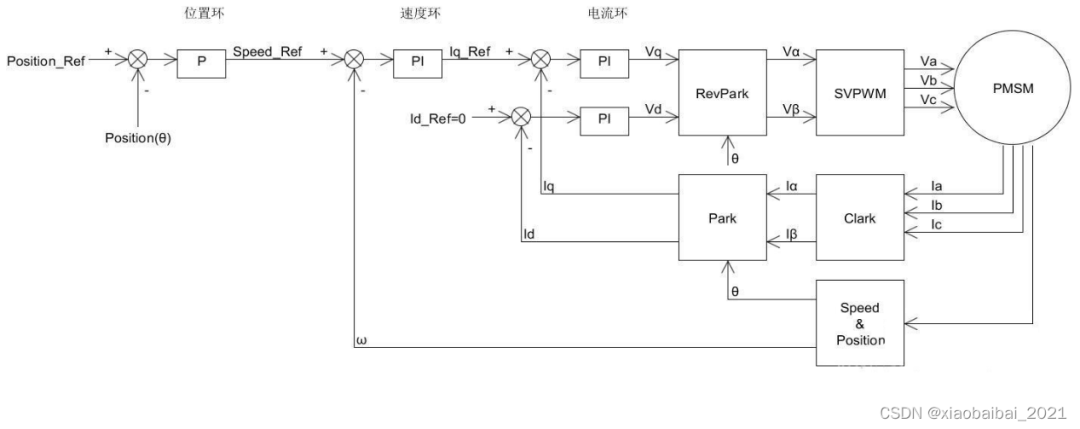
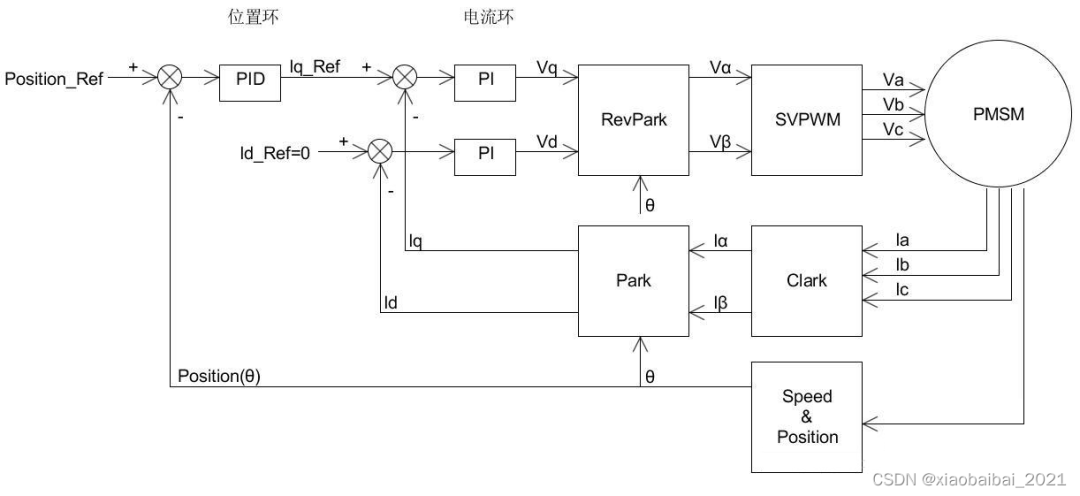
当我们在上述系统中,再增加位置控制的P环节后,变成了如下框图形式,三环控制:
在实际使用中有时候电机的转速很低时,角速度ω的测量不精确,系统中的速度环会带来较大误差。此时可以不用速度环,而只用位置和电流双环控制:
(注意这里的位置环用上了完整的PID环节,是因为位置的微分就是速度,引入微分环节可以在不使用速度误差的情况下改善速度控制)
好了,关于无刷电机FOC矢量控制的入门知识,就讲到这里了。










暂无评论