关键要点

将复杂的电路理解为串联和并行连接的组合。

线性的概念及其在电路分析中的应用。

用来快速有效地表示等效电路的附加方法。

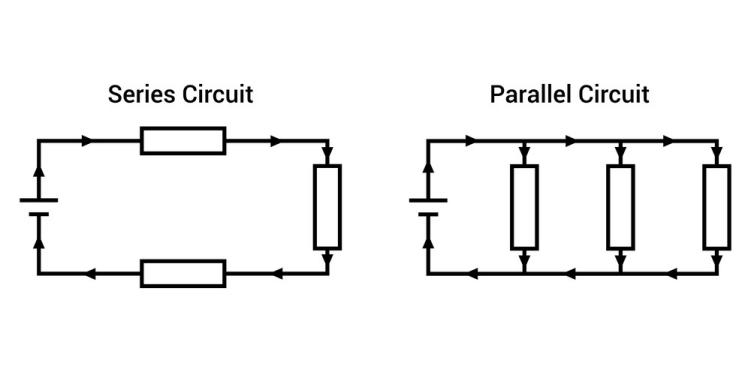
复杂电路包括串联和并联元件，在这里分别显示

电路设计是一门广泛的学科，它结合了许多数学分析和电磁学的方法。在该理论发展的早期，设计师会遇到电路的基本构建模块以及电路简化的入门协议。虽然这些是电路的基础，并且几乎适用于任何电路，但还有很多情况需要更复杂的描述。复杂的电路提供了一个额外的挑战，因为它们需要更高级的技术才能得到一个可以通过人类或机器进行分析的网络。学习这些程序为设计师提供了更多的电路分析机制，并更全面地理解了网络设计。

节点分析：串联和并联连接

在任何新兴工程师的工具箱中，等效电路简化都是最重要的解决方法之一。将复杂电路网络简化为单一的代表性电路元件的能力是电路建模和分析的核心方法。首先，定义电路拓扑的一个基本方面十分重要：串联和并联。理解这些相关概念的最佳方法是跟踪电流的流动：

串联：电流流经电路中的元件时，它们会连成一条线，没有任何分支。换句话说，该特定电路或子电路中不存在分支电流路径。在网络分析方面，连续串联的元件共享一个节点或参考点。

并联：电流从源头分配到多个分支路径上。对于任何有两个端口的并联元件，两个节点都与其它并联的两个端口元件共通。

除了基础电路之外, 几乎很少有完全串联或并联的整体电路。相反, 大多数电路包含不同数量的串联和并联元件，以利用这两种连接方法的不同性能特征。复杂的电路，或包含并联和串联元件的电路，更为常见。在分析方面，评估一个由串联元件组成的电路通常比一个并行电路更直接，尽管这个规则有明显的组件例外。大多数级数元素都是单个元素的总和——为了找到纯级数网络的阻力，只需添加循环中包含的值。平行元素的和不那么直观：平行相加，取单个分量的倒数和的倒数。如所描述的串联和并联计算都适用于电阻器和电感器，但电容器是该框架的一个显著的例外。虽然电容器确实有规律地和相互求和，但它们的应用是交换的：串联电容器相互求和，而传统的并联电容器相互求和。在分析电路时，尽管有明显的组件例外，评估由串联元件组成的电路通常比并联电路更为直观。大多数串联元件是各个元素的总和：要找到纯串联网络的电阻，只需将循环内包含的值相加即可。并联元件的总和则不那么直观：要进行并联，需要对各个组件的倒数之和取倒数。上述串联和并联计算适用于电阻器和电感器，但电容器则例外。虽然电容器通常可以进行常规的倒数求和，但它们的应用是相反的：串联电容器进行倒数求和，而并联电容器则进行常规求和。

使用基尔霍夫定律进行节点分析

也可以从电压和电流方面分析串联和并行配置。串联组件，作为同一分支，具有相同的电流，但在每个非源电路元件的电压降，如基尔肖夫的环路定律概述。同时，由于基尔肖夫的结规则，并联组件具有相同的电压，但有不同的电流，即进入一个节点的总电流必须等于一个节点的总电流。更正式地说，串联元件和并联元件可以分别被描述为分压器和分流器。这些电路操作根据组件的相对值提供电压或电流的比例分布；例如，两个相同的电阻会经历相同的电压降（串联）或相同的电流（并联），因为它们的电阻为1：1值。对于不同的值，较大（或最大）的元件代表电流或电压的最大比例，反之亦然。在电路中，我们可以通过电压和电流的角度来分析串联和并联配置。如基尔霍夫环路定律所述，串联元件在同一电路中，拥有相同的电流，但每个非提供电流的电路元件都会产生一定的电压降。与此同时，并联元件拥有相同的电压，但由于基尔霍夫节点定律所示，不同的电流会进入和流出节点，使它们的电流不同。 从更正式的角度讲，串联和并联元件可以被描述为电压分压器和电流分流器，分别提供基于元件相对值的电压或电流的比例分配；例如，两个相同的电阻器在串联时将经历相同的电压降，而在并联时将经历相同的电流，因为它们具有1：1的电阻值。

复杂电路简化的构建

复杂性的话题需要与线性和叠加相结合。线性描述了系统的整体行为，即从输入到输出的映射，而叠加是线性系统的决定条件。为了保持叠加，系统必须在整个输入范围内维持可加性和齐次性：可加性 ：两个单独输入的组合输出与组合输入的总和输出相同。更常见的是，可以表示为等式：

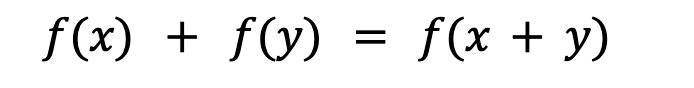
*假设x和y是f域内的元素。

齐次性：输入端的标量乘以某个值，等价于输出端相应标量乘以该值。同样，这需要一个更常见的等式：f (sx) = sf (x)

*对于所有元素s，x在f的域内。

回到一个电路的复杂性，叠加，特别是可加性特性，是一个系统的输入和输出之间的关系。复杂电路是并行元素和串联元素的混合物，它们的解代表了这两种连接方法的适当贡献。为了进一步推动这种关系，复杂电路代表了平行和串联元件的组成，在非正式和数学上；在节点分析的背景下，电气工程师参考叠加理论，以区分更一般和数学的叠加原理的弯曲。这两个元素的组合形成了叠加原理的基础并定义了一个线性系统。总体而言，线性的适用范围有限，是对系统真实行为的简化，但在它适用的情况下，它是一种强有力的工具来建模。有利的是，线性系统可以用各种数学函数、变换和算子来分析，并且比非线性系统更容易求解。回到电路的复杂性，叠加原理，特别是可加性特性，是系统输入和输出之间的关系。如前所述，复杂电路是并联和串联元素的组合，并且它们的解决方案代表了两种连接方法的结合。

评估不那么直观的网络

事实上，许多网络可以通过串联求和并行求和。人工分析应缓慢而仔细地进行，以确定两个元素之间的关系，以及适当的顺序，以在计算中保留串联或并联组件的性质。然而，并不是每一种电路排列都易于串联或并联的识别，需要利用各种转换来更好地说明电路内的关系。一般来说，星形变换多边形用于减少特定电路中的节点数量，尽管其实现有一个实际的限制，即元素的替换数量受到以下限制：

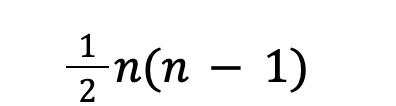
*对于n个元素数。

最有用的情况是当n = 3时，因为转换后的网络具有与原始网络相同数量的元素，但也应该提到其他值。使用小于3个元素的转换将生成具有更少组件的模型，而使用大于3个元素的转换将增加组件的总数，同时减少节点数。前者的使用范围有限，而后者只会使分析复杂化。回到特殊的n = 3的情况下，在一些情况下，设计师可能会遇到非正统的网络结构。虽然在捕获的示意图中不太常见，但它们仍然可以在三个元素的节点交点上找到，比如在桥中发现的那些元素。这些转换的形式上是基于网络的视觉形状的Y-Δ（delta）或T-π（pi）转换，它们利用组件之间的级数和并行关系来创建所有三个元素之间的比例。删除节点允许将电路重新解释为串联或并联连接，进一步强调了在复杂电路分析中进行变换的优势。

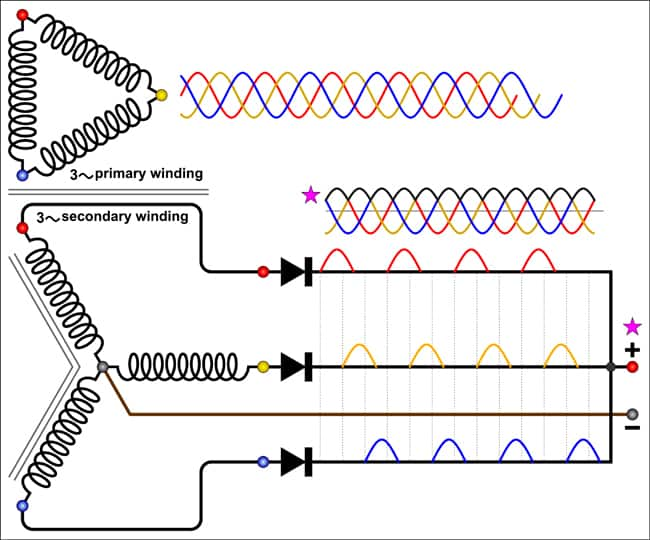
 Δ-Y变换通常与三相电力系统有关

进一步降低复杂性的等效电路模型

复杂电路的简化有时需要使用额外的算法来产生可工作的拓扑结构。最初为由电流源、电压源和电阻器组成的线性直流电路设计的这两种方法，可通常适用于固定频率的线性交流电路：费温定律：将电路替换为一个等效电压源和串联电阻，测量开路电压。将电路转换为费温定理等效电路的三个步骤如下：

1. 确定等效电压(Vth)，即输出端测量的电压。通常，这是通过使用已知的源电压和电压分压计算来确定留在输出端的源电压的分数来实现的。注意，打开电路（其中负载与等效电路隔离）会导致某些支路没有电流流动。

2. 通过从输出端子的电路来确定等效电阻（Rth）。这个电阻是通过假设所有电源的理想电阻，即电压源的理想电阻为零，电流源的理想电阻为无穷大，并将它们分别替换为开路和短路。

3. 最后，费温等效电路可以用Vth的电压源和Rth的串联电阻来表示。

Mayer-Norton电路理论-用等效电流源和并联电阻(从负载角度)替代电路。作为Thévenin等效性的对立面，实现Mayer-Norton等效电路需要遵循三个步骤:

1.通过在负载处短路终端来找到等效电流(Ino)。首先找到总电流(通常使用欧姆定律，但其他方法也可获得更快的结果)。一旦找到总电流，则计算输出短路电流。

2.与Thévenin等效电路一样，通过用短路和开路替换源，从输出端评估等效电阻。

3.从负载处观察，Mayer-Norton等效电路显示为电流源Ino和并联电阻Rth。

Thévenin和Mayer-Norton代表一种双重方法，通常在电子学中看到，其中任一使用互补的模式提供等效性。尽管线性电路只占工程师和设计师将遇到的拓扑结构的一小部分，因为符合框架的设备数量有限，但等效电路具有相关源的附加用例。通常，当确定等效电压或电流时，电压和电流源将被替换为短路和开路，但不能轻易忽略相关源。相反，设计师可以将测试源连接到输出端，并计算所得到的电流或电压。

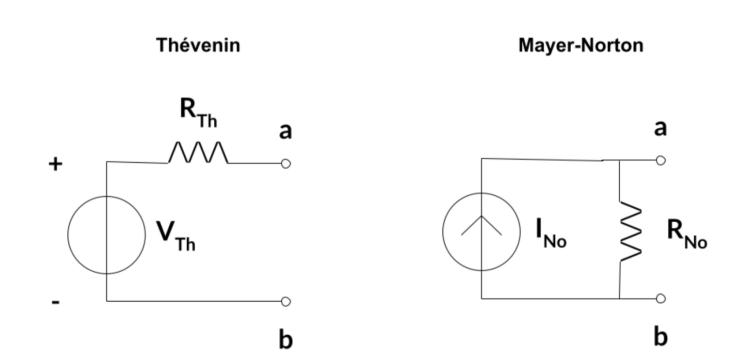
 两种等效电路模型的比较。

复杂电路简化存在的目的是为工程师和设计师提供各种算法，以简化电路设计过程。能够用简单的实践方法测量广泛网络的响应，极大地提高了网络分析的可读性。此外，这些方法构成了电子节点分析的基础，这对电路模拟非常必要。

Cadence的PCB设计和分析软件提供了全面的设计和分析工具包，具备满足最严格的板子规格的广泛功能。对于布局，OrCAD PCB Designer提供了强大的功能，可以满足当今全功能板的需求，并推动未来设计的创新。Cadence Allegro PCB Designer是一个完整的、高性能印制电路板设计套件。通过顶尖的技术，它为创建和编辑复杂、多层、高速、高密度的印制电路板设计提供了一个交互式、约束驱动的设计环境。它允许用户在设计过程的任意阶段定义、管理和验证关键的高速信号，并能抓住今天最具挑战性的设计问题。AllegroPCB Designer提高了设计效率和缩短设计周期，让你的产品尽快进入量产。