引言
光子具有低噪声、高速度和长距离传输的能力,是前景广阔的量子信息载体。然而,单个光子之间缺乏直接相互作用一直是实现确定性多光子门和量子模拟器等先进光子量子技术的主要障碍。一种方法是利用测量诱导的非线性,但这种方法本质上是概率性的。另一种确定性方法是利用光物质与原子或量子点等量子发射器的相互作用。
本文将探讨结合这两种方法的新实验平台--基于嵌入纳米光子波导中的可调量子点发射器的可编程非线性量子光子电路。该平台能够在几光子水平上实现可编程线性光学和可调谐确定性非线性光学。

可编程非线性光子电路
如图 1b 所示,关键部件是嵌入砷化镓芯片光子晶体波导中的 InAs 量子点(QD)。量子点是一种可调非线性介质,用于介导从其上散射的光子之间的相互作用。
整体电路布局如图 1a 所示。光子被编码为两种时间模式或 “时间区间”,分别标为早期(E)和晚期(L)。这些光子在两个可调马赫-泽恩德干涉仪中进行线性运算,该干涉仪通过一个自稳定时带干涉仪实现(图 1c)。
在线性干涉仪之间,光子通过光子晶体波导与 QD 相互作用,实现可调非线性操作。线性和非线性操作可通过以下方式独立编程:
1.利用直流斯塔克效应调谐 QD 与光子之间的光谱失谐 Δ,以控制非线性强度。
2.调整光子脉冲相对于 QD 线宽的时间带宽。
3.设置线性干涉仪的反射率和相对相位ϕ。
这种线性和非线性组件的可编程性是该平台的一个关键功能。
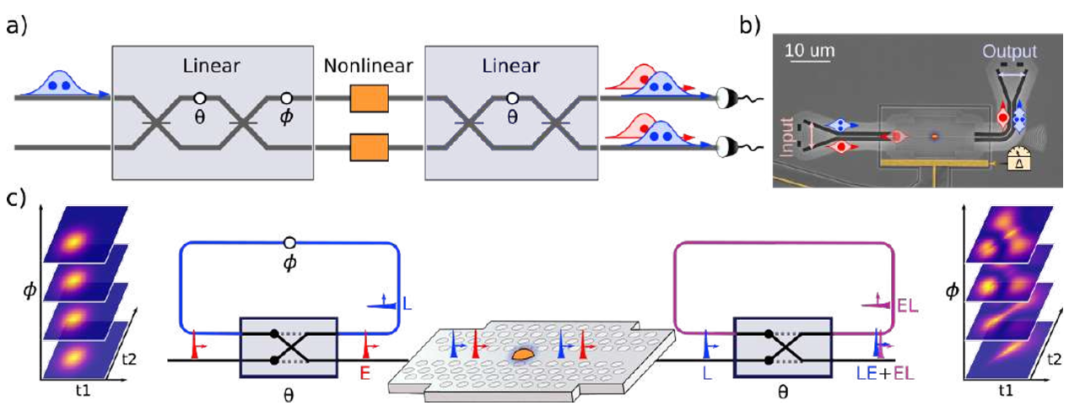 图 1:可编程非线性量子光子电路示意图
图 1:可编程非线性量子光子电路示意图
a) 电路包括可调谐量子点(QD)非线性变换与使用分时马赫-泽恩德干涉仪的可控线性光学电路交错。注入电路的光子通过线性和非线性操作发生干涉和相互作用,并利用 SNSPD 记录传输的光子。
b) SEM 图像显示,砷化镓纳米光子器件通过光子晶体波导中的砷化镓 QD 散射光子来实现非线性相互作用。光栅耦合器处理光子的输入和输出耦合,电极(黄色突出显示)控制 QD 的电场,通过直流斯塔克效应调整非线性相互作用。
c) 线性光学装置在时域中对光学模式进行编码,包括早期(E)和晚期(L)时间带。时域干涉仪将 E 模和 L 模耦合在一起,增加了一个相对相位 (j)。光子在 1.6K 低温恒温器中与 QD 相互作用,在 E 和 L 时间出现非线性。干涉仪中的重组模式会受到线性和非线性相位的干扰,从而改变光子的特性,如理论联合时间强度 (JTI) 插图所示,在不同的 ϕ 设置下,有非线性相互作用和无非线性相互作用。
线性和非线性操作特征
如图 2a 所示,通过测量输出光子的联合时间强度 (JTI),对可编程线性和非线性操作进行了表征。在 QD 远失谐(Δ ≫ σ)的情况下,JTI 中观察不到相关性,这与线性光学相对应。当 QD 调谐到共振时,沿对角线会出现强相关性以及单光子项产生的干涉条纹。
线性和非线性操作的相互作用在图 2b 中更加明显,该图绘制了两个光子在第一模式中的输出概率与线性相位 j 的关系。当 QD 远距离失谐时(线性光学),会观察到高可见度的干涉。当 QD 调谐到共振时,非线性相移会降低条纹的可见度。
根据等式 1-2 中的变换,非线性操作模型为非线性相位 φNL 和散射概率 lNL。图 2c 显示了提取的 φNL 和 lNL 与失谐 Δ 的关系,表明非线性强度具有广泛的可调性。
图 2d 比较了非线性散射概率与其他方法(如测量引起的非线性和优化的单面波导设计)的关系。确定性波导-QD 平台的性能优于测量诱导方案,并能通过优化波导设计达到统一散射概率。
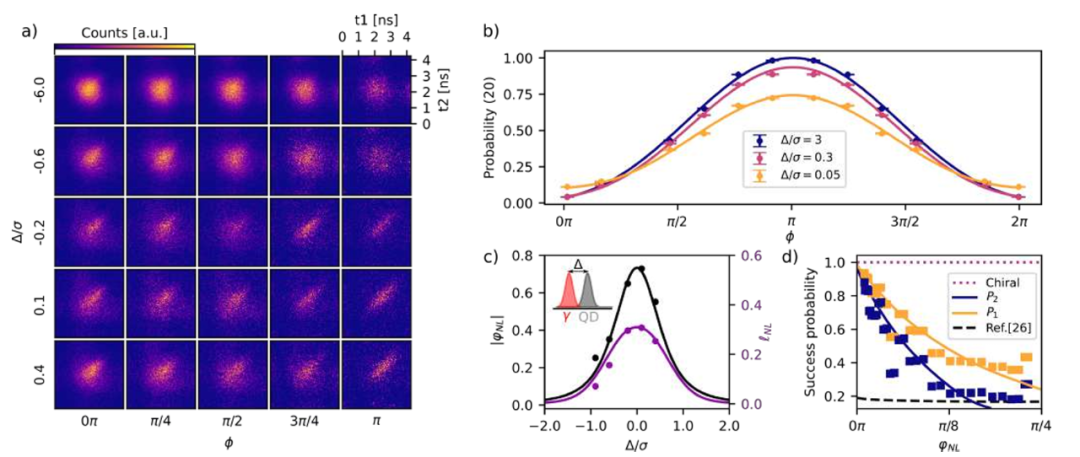 图 2:线性和非线性光子操作的可编程性
图 2:线性和非线性光子操作的可编程性
a) 来自输出光子时间分辨相关测量的实验归一化联合时间强度数据。列表示干涉仪的不同线性相位设置,行表示控制非线性强度的各种 QD 调谐。测量使用 700 ps 输入脉冲。
b) 电路中不同非线性的干涉测量。输出配置 |20⟩ 的概率显示为控制非线性强度的各种解谐 ∆ 值的线性相位 ϕ 的函数。误差条代表 1 个标准偏差,假设为泊松子光子统计。
c) 非线性相位和散射概率参数与解谐 ∆ 的关系。黑色和紫色数据分别代表非线性相位和散射概率,是将测量到的光子统计量拟合到非线性变换模型中得到的。插图: 入射光子 (γ) 与控制非线性的 QD 之间的失谐 ∆。
d) 单光子(黄色)和双光子(蓝色)成分散射后的传输概率与实施的非线性相位 φNL 的比较。标记为实验数据,实线为模拟系统参数的理论值。其他曲线显示了手性或单面波导散射(紫色虚线)和基于测量的优化线性光学方案(黑色虚线)的结果。
非谐波分子动力学量子模拟
作为一个应用实例,可编程非线性电路用于模拟 H2O 分子的振动量子动力学,包括关键的非谐波效应,如图 3a 所示。
模拟将分子振动模式映射到光学模式上,单声子激发与单光子相对应(图 3b)。分子初始化时在一个局部振动伸展模式中有两个声子,对应于一个光学模式中的两个光子。
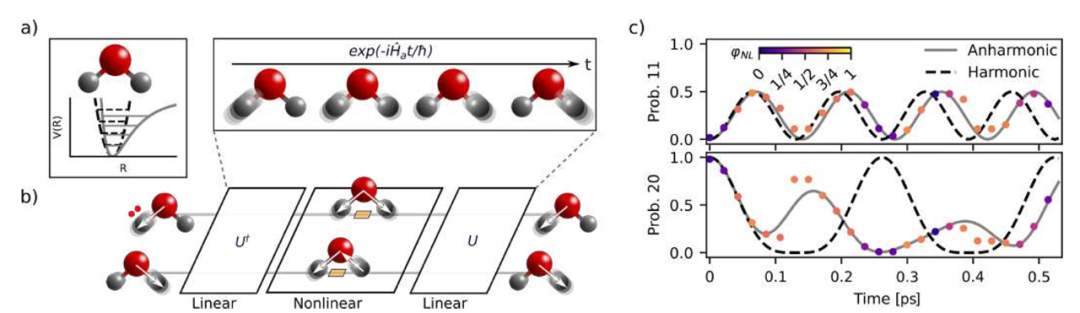
图 3: 利用可编程非线性光子量子电路对 H2O 振动动力学进行量子模拟
a) 振动自由度的分子势图解,一般为非谐波(实线),谐波近似(虚线)并不能很好地反映振动自由度。
b) 通过将光学模式与振动模式、光子与声子联系起来,将分子的量子振动动力学映射到光子系统中。非谐波哈密顿动力学(上插图)通过矩阵变换 U 在局部基和正态基之间转换,在正态基中演化,然后通过 U† 转换回来。在光子实现中,电路的线性部分执行基变化和谐波演化,而非线性相互作用(黄色方框)执行非谐波演化。
c) H2O 非谐波动力学量子模拟的实验结果,初始化时两个光子处于相同的局部拉伸模式。顶部和底部面板分别显示了以不同或相同局部拉伸模式出现激发的配置输出占位。数据符合理论模型(实线),并与谐波近似预测(虚线)进行了比较。数据标记按每个演化时间步的非线性相位强度(插图中的刻度条)进行颜色编码。
然后,电路在模拟的每个短时间步中执行以下序列:
1.线性操作将初始局部模式映射到正常振动特征模式。
2.根据分子参数设置适当的线性 ϕ 和非线性 φNL 相,在正常模式基础上实现非谐波演化。
3.第二次线性运算映射回局部模式基础。
4.在输出端进行光子计数,得出各局部模式的最终声子分布。
根据图 2c 中的特征描述,通过调整 QD 调谐 Δ 来编程非线性相位 φNL。图 3c 显示了包括非谐波效应(实线)在内的模拟种群动态,与谐波近似(虚线)有很大偏差。与理论的极佳一致性证明了在该平台上进行可编程非谐波分子动力学模拟的能力。
讨论与未来方向
实现可编程非线性量子光子电路的这一开创性实验为量子光子学带来了许多新机遇。确定性非线性功能能够实现线性光学所难以实现的关键功能,如光子量子门、贝尔态分析器、量子非拆卸探测器和非高斯态合成。
展望未来,基于时序复用技术进一步扩展非线性电路,可以模拟更大的分子系统,其计算优势超过经典方法。在手性波导或单面波导上实施建议的方案,可以消除残余损耗,从而实现完全确定的非线性操作。
可编程非线性量子光子电路提供了强大的新平台,在量子计算、模拟、传感等领域具有多种潜在应用。本文介绍了这一新兴功能及其首次实验演示。随着该技术的进一步发展,它将改变量子光子技术的面貌








暂无评论