一般在用运放时，规格书中有带宽BW的指标，也有压摆率SR的指标。两个参数看起来都是和时间有关的，但应用场景是不同的。

比如阶跃大信号输入的时候，输出响应是受到BW限制，还是SR的影响？如果阶跃输入信号的幅值是1V，输出响应一般是受到SR的影响；如果阶跃输入信号在10mv左右，是小信号，这个时候输出响应受到带宽BW的限制。但这种所谓的大信号和小信号输入，其幅值大小是相对的，因此定量讨论，区分大信号和小信号幅值是很有必要的。

对于一个同相放大器，给一个阶跃激励。设定幅值是Vin-max，此时在不知道幅值大小的情况下，就不知道输出响应是受BW还是SR的制约。

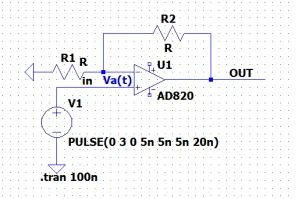
对于理想的运放，输出Vout=(1 R2/R1)*Vin，这个公式根据负反馈的虚短虚断很容易得到。但前提是理想运放，无论输入信号Vin的频率怎么变化，运放的开环增益Aol始终都是无穷大，但显然实际运放是没有这个能力的。当输入信号达到一定频率的时候，开环增益Aol开始滚降，一般在工程应用分析的时候，实际运放都会看作单极点模型，那么Aol就会以20dB/dec的速度滚降。

从LM358的规格书可以看出，无论是开环增益，还是闭环增益，都是受到信号频率的制约，不会按照理想运放闭环放大倍数的G=1 R2/R1进行信号放大。

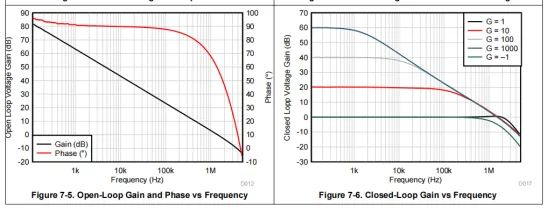
上述的增益vs频率的曲线，并没有体现压摆率SR和带宽GB两者在输入信号幅值大小的区别。讨论输入阶跃信号的响应，就要从频域的角度出发，不能简单的将运放同相和反相端虚短看待，所以两端之间的电压Va(t)也就不会一直是0。通过查阅资料，知道输出响应和输入阶跃激励Vin-max之间的关系，对于线性电路，此时无论输入阶跃信号是什么幅值，输出响应都有统一的表达式：

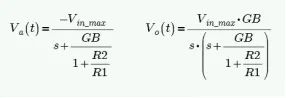
随后将上述表达式利用拉氏变化，可以达到时域的表达式，就能找到输入幅值大小对输出响应的影响了。当时间t=0，输出电压=0；t>0，输出电压开始指数变化；当t趋于无穷大，也就是输出电压稳定的时候，此时输出电压就满足理想同相放大器的特性了，Vout=(1 R2/R1)*Vin-max。

通过数学公式，清晰明了的知道电路的变化过程。尽管t趋于无穷大是发生不了的事件，但知道输出电压不会马上跟随输入激励的变化而变化，是有一个指数变化的过程。

指数变化的时间常数τ=(1 R2/R1)/GB。

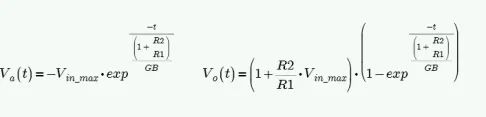
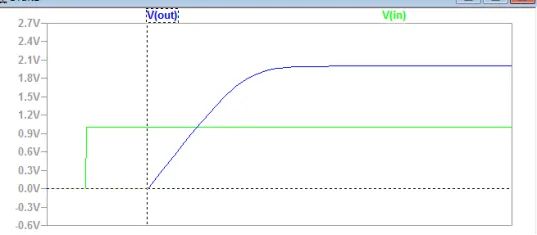
指数最大的变化率（斜率最大的时刻）也就是上图光标所在的位置，发生在t=0的时刻，通过对输出电压函数求导dVo(t)/dt=Vin-max*GB，输出电压的最大斜率就是输入激励幅值和带宽之积，所以输入阶跃的幅度Vin-max足够小；否则一个突然施加的Vin-max*G会在t=0时刻，从而过驱动，让运放从线性工作模式进入到非线性工作模式。一旦进入非线性工作模式，上文推导的频域函数和时域函数就不适用了。

当输入Vin-max增大，运放进入非线性工作模式，那么输出响应就不再是指数输出，就是快速的线性输出，此时的变化率就是压摆率SR。所以，运放在线性的工作模式，运放的带宽制约输出响应幅度。运放在非线性的工作模式，运放的压摆率制约输出响应幅度。

至此就得到了SR和GB之间的关系，当Vin-max*GB < SR时，运放的带宽制约输出响应幅度；反之，当Vin-max*GB > SR时，运放的压摆率制约输出响应幅度。前文提到运放的规格书都会给出GB和SR的参数，所以利用这两个参数，就能算出输入激励的Vin-max大小，从而合理的设计电路。