1 PID神经元网络结构
PID神经元网络从结构上可以分为输入层、隐含层和输出层三层,n 个控制量的 PID神经元网络包含 n个并列的相同子网络,各子网络间既相互独立,又通过网络连接权值相互联系每个子网络的输入层有两个神经元,分别接收控制量的目标值和当前值。每个子网络的隐含层由比例元积分元和微分元构成,分别对应着 PID 控制器中的比例控制积分控制和微分控制。PID神经元网络按被控系统控制量的个数可以分为控制单变量系统的单控制量神经元网络和控制多变量系统的多控制量神经元网络。其中单控制量神经元网络是 PID神经元网络的基本形式,多控制量神经元网络可以看成是多个单控制量神经元网络的组合形式。单控制量神经元网络的拓扑结构如图所示。

图中,X1是控制量的控制目标,X2是控制量当前值,Y是神经元网络计算得到的控制律,wij和wjk是网络权值,从中可以看到单控制量神经元网络是一个三层前向神经元网络,网络结构为2一3一1,隐含层包含比例元积分元和微分元三个神经元。多控制量神经元网络可以看成多个单控制量网络的并联连接,多控制量神经元网络拓扑结构如下图所示。
图中,X11,X21,...,Xn1是控制量的控制目标;X12,X22,...,Xn2是控制量的当前值;Y1,Y2,···,Yn是多控制量神经元网络计算得到的控制律;wij和wjk是网络权值。

2 控制律计算
PID 神经元网络分为输入层、隐含层和输出层,网络输入量为控制量当前值和控制目标,输出量为控制律,各层输人输出计算公式如下。
(1)输入层
输人层中包含2n个神经元,输出数据xsi等于输人数据Xsi计算公式为

(2)隐含层
隐含层有 3n个神经元,包括n个比例神经元个积分神经元和个微分神经元这些神经元的输人值相同,计算公式为

(3)输出层
输出层有n个神经元构成n 维输出量输出层的输出为隐含层全部神经元的输出值加权和,计算公式如下:

3 权值修正
PID神经元网络在控制的过程中根据控制量误差按照梯度修正法修正权值,使得控制量不断接近控制目标值,权值修正的过程如下。
误差计算公式如下

4 控制对象PID神经元网络的控制对象是一个3输人3输出的复杂合系统系统的传递函数如下

5 模型建立
PID神经元网络控制器和被控系统构成的闭环控制系统如图所示

6 编程仿真结果
1)控制效果

2)输入曲线

3)控制误差

7 程序仿真
%% 该代码为基于PID神经网络的系统控制算法% 清空环境变量clcclearclose all
%% 网络结构初始化rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二个控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出
%权值初始化k0=0.03;
%第一层权值w11=k0*rand(3,2);w12=k0*rand(3,2);w13=k0*rand(3,2);%第二层权值w21=k0*rand(1,9);w22=k0*rand(1,9);w23=k0*rand(1,9);
%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定
%% 网络迭代优化for k=1:1:200
%% 控制量输出计算 %--------------------------------网络前向计算-------------------------- %系统输出 y1(k)=(0.4*y_1(1) u_1(1)/(1 u_1(1)^2) 0.2*u_1(1)^3 0.5*u_1(2)) 0.3*y_1(2); y2(k)=(0.2*y_1(2) u_1(2)/(1 u_1(2)^2) 0.4*u_1(2)^3 0.2*u_1(1)) 0.3*y_1(3); y3(k)=(0.3*y_1(3) u_1(3)/(1 u_1(3)^2) 0.4*u_1(3)^3 0.4*u_1(2)) 0.3*y_1(1); r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标 %系统输出限制 yn=[y1(k),y2(k),y3(k)]; yn(find(yn>ynmax))=ynmax; yn(find(yn
%比例神经元P计算 xp=[x1i(1),x2i(1),x3i(1)]; xp(find(xp>xpmax))=xpmax; xp(find(xp
%积分神经元I计算 xi=[x1i(2),x2i(2),x3i(2)]; qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)]; qi=qi_1 xi; qi(find(qi>qimax))=qimax; qi(find(qi
%微分神经元D计算 xd=[x1i(3),x2i(3),x3i(3)]; qd=[0 0 0]; xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)]; qd=xd-xd_1; qd(find(qd>qdmax))=qdmax; qd(find(qd
%输出层计算 wo=[w21;w22;w23]; qo=[h1i',h2i',h3i'];qo=qo'; uh=wo*qo; uh(find(uh>uhmax))=uhmax; uh(find(uh
%调整w21 Sig1=sign(ypc./(uhc(1) 0.00001)); dw21=sum(error.*Sig1)*qo'; w21=w21 rate2*dw21; %调整w22 Sig2=sign(ypc./(uh(2) 0.00001)); dw22=sum(error.*Sig2)*qo'; w22=w22 rate2*dw22; %调整w23 Sig3=sign(ypc./(uh(3) 0.00001)); dw23=sum(error.*Sig3)*qo'; w23=w23 rate2*dw23;
%输入层和隐含层权值调整 delta2=zeros(3,3); wshi=[w21;w22;w23]; for t=1:1:3 delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t) 0.00000001)); end for j=1:1:3 sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j) 0.00001)); end s1=sgn'*[r1(k),y1(k)]; wshi2_1=wshi(1:3,1:3); alter=zeros(3,1); dws1=zeros(3,2); for j=1:1:3 for p=1:1:3 alter(j)=alter(j) delta2(p,:)*wshi2_1(:,j); end end for p=1:1:3 dws1(p,:)=alter(p)*s1(p,:); end w11=w11 rate1*dws1;
%调整w12 for j=1:1:3 sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j) 0.0000001)); end s2=sgn'*[r2(k),y2(k)]; wshi2_2=wshi(:,4:6); alter2=zeros(3,1); dws2=zeros(3,2); for j=1:1:3 for p=1:1:3 alter2(j)=alter2(j) delta2(p,:)*wshi2_2(:,j); end end for p=1:1:3 dws2(p,:)=alter2(p)*s2(p,:); end w12=w12 rate1*dws2; %调整w13 for j=1:1:3 sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j) 0.0000001)); end s3=sgn'*[r3(k),y3(k)]; wshi2_3=wshi(:,7:9); alter3=zeros(3,1); dws3=zeros(3,2); for j=1:1:3 for p=1:1:3 alter3(j)=(alter3(j) delta2(p,:)*wshi2_3(:,j)); end end for p=1:1:3 dws3(p,:)=alter2(p)*s3(p,:); end w13=w13 rate1*dws3;
%参数更新 u_3=u_2;u_2=u_1;u_1=uh; y_2=y_1;y_1=yn; h1i_1=h1i;h2i_1=h2i;h3i_1=h3i; x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;end
%% 结果分析time=0.001*(1:k);figure(1)subplot(3,1,1)plot(time,r1,'r-',time,y1,'b-');title('PID神经元网络控制','fontsize',12);ylabel('控制量1','fontsize',12);% legend('控制目标','实际输出','fontsize',12);legend('控制目标','实际输出');
subplot(3,1,2)plot(time,r2,'r-',time,y2,'b-');
ylabel('控制量2','fontsize',12);legend('控制目标','实际输出');subplot(3,1,3)plot(time,r3,'r-',time,y3,'b-'); xlabel('时间(秒)','fontsize',12);ylabel('控制量3','fontsize',12);legend('控制目标','实际输出');
figure(2)plot(time,u1,'r-',time,u2,'g-',time,u3,'b');title('PID神经网络提供给对象的控制输入');xlabel('时间'),ylabel('被控量');legend('u1','u2','u3');gridfigure(3)figure(3)plot(time,J,'r-');axis([0,0.2,0,1]);gridtitle('控制误差曲线','fontsize',12);xlabel('时间','fontsize',12);ylabel('控制误差','fontsize',12);


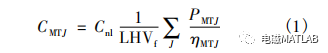
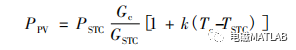






暂无评论