1 理论介绍

在图11-1(a)所示的网络中，供电点A通过馈电干线向负荷节点b、c和d供电，各负荷节点功率已知。如果节点d的电压也给定，就可以从节点d开始，利用同一点的电压和功率计算第三段线路的电压降落和功率损耗，得到节点c的电压，并算出第二段线路末端的功率，然后依次计算第二段线路和第一段线路的电压降落和功率损耗，一次性地求得解答。但是实际的情况并不这么简单，多数的情况是已知电源点电压和负荷节点的功率，要求确定各负荷点电压和网络中的功率分布。在这种情况下，可以采取近似的方法通过迭代计算求得满足一定精度的解答。

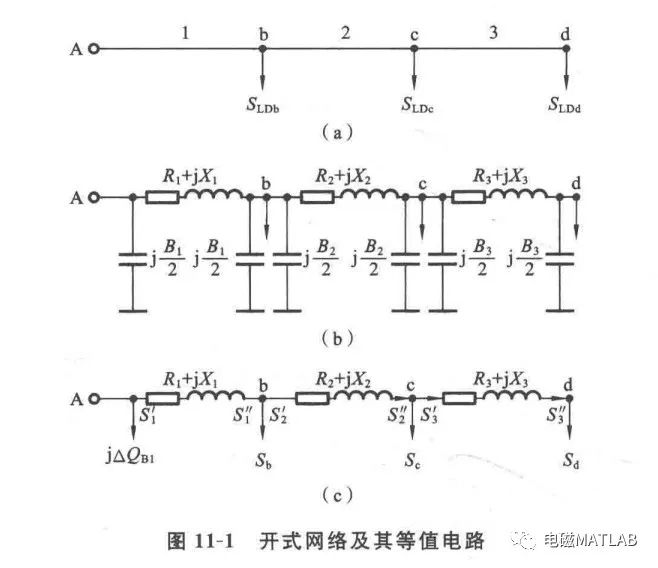
在进行电压和功率分布计算以前，先要对网络的等值电路（见图11-1(b))作些简化处理。具体的做法是，将输电线等值电路中的电纳支路都分别用额定电压U、下的充电功率代替，这样，对每段线路的首端和末端的节点都分别加上该段线路充电功率的一半。

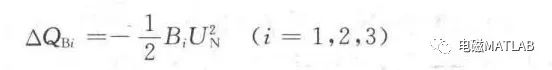
习惯上称S、S。和S:为电力网的运算负荷。这样，我们就把原网络简化为由三个集中的阻抗元件相串联，而在四个节点（包括供电点）接有集中负荷的等值网络（见图11-1(c))。针对图11-1(c)所示的等值网络将按以下两个步骤进行电压和功率分布的计算。第一步，从离电源点最远的节点d开始，利用线路额定电压，逆着功率传送的方向依次算出各段线路阻抗中的功率损耗和功率分布。对于第三段线路

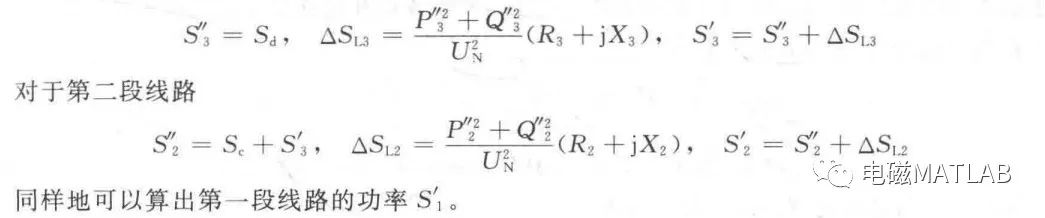
2 算例

1）IEEE33节点算例结构

2）负荷时序值

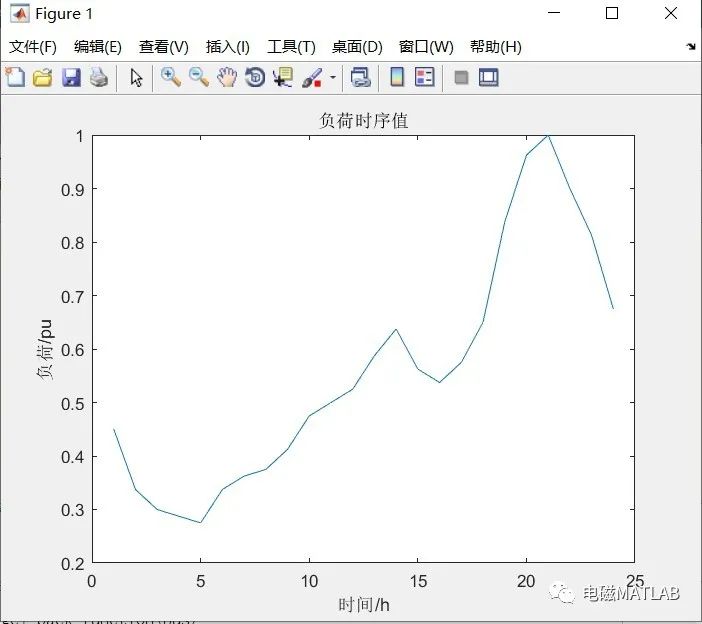
3 程序运行结果

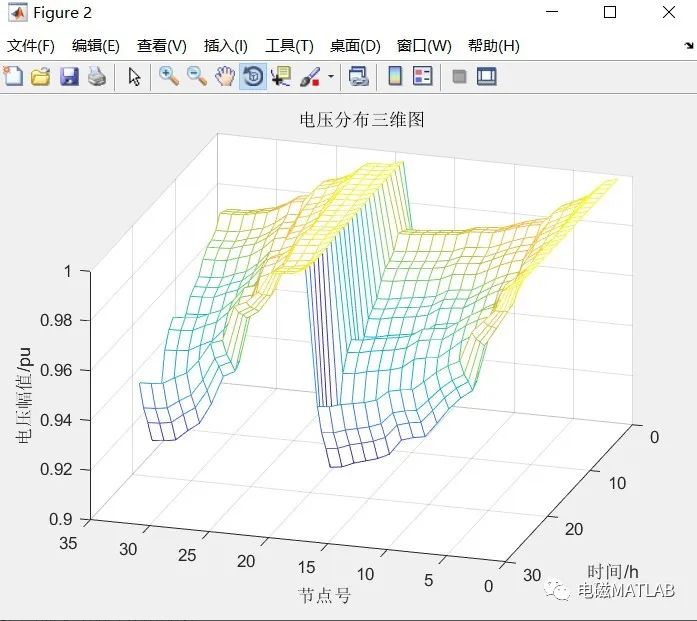
4 matlab程序

1）主函数

clcclearclose all
%% 日前负荷时序值load=[0.450000000000000,0.337500000000000,0.300000000000000,0.287500000000000,0.275000000000000,0.337500000000000,0.362500000000000,0.375000000000000,0.412500000000000,0.475000000000000,0.500000000000000,0.525000000000000,0.587500000000000,0.637500000000000,0.562500000000000,0.537500000000000,0.575000000000000,0.650000000000000,0.837500000000000,0.962500000000000,1,0.900000000000000,0.812500000000000,0.675000000000000];
figureplot(load)xlabel('时间/h')ylabel('负荷/pu')title('负荷时序值')

%% 前推回代法算潮流v=zeros(33,24);for t=1:24%% 系统负荷参数 节点  有功  无功Bus=[1,0,0   ;2,100, 60;3,90,40;4,120,80;5,60,30;6,60,20;7, 200, 100 ;8,200,  100 ;9, 60, 20;10,60, 20;11,45,30;12,60, 35;13,60, 35;14,120,80;15,60, 10;16,60, 20;17,60, 20;18,90, 40;19,90, 40;20,90, 40;21,90, 40;22,90, 40; 23,90, 40; 24,420, 200;25,420, 200 ;26,60, 25;27,60 ,25;28,60, 20;29,120, 70;30,200,600 ;31,150, 70;32,210, 100 ;33,60,40;];%% 负荷更新  Bus(:,2)=load(t)*Bus(:,2);  Bus(:,3)=load(t)*Bus(:,3);  %% 计算潮流[voltage]=back_function(Bus);v(:,t)=voltage;end%% 标幺化v=v/12.66;%% 输出figuremesh(v')ylabel('时间/h')xlabel('节点号')zlabel('电压幅值/pu')title('电压分布三维图')

2）子函数

function [voltage]=back_function(Bus)%% 前推回代法%% 系统支路参数  节点  节点  电阻  电抗Branch=[1 ,1 ,2 ,0.0922,0.0407;2 ,2 ,3 ,0.4930,0.2511;3 ,3 ,4 ,0.3660,0.1864;4 ,4 ,5 ,0.3811,0.1941;5 ,5 ,6 ,0.8190,0.7070;6 ,6 ,7 ,0.1872,0.6188;7 ,7 ,8 ,0.7144,0.2351;8 ,8 ,9 ,1.0300,0.7400;9 ,9 ,10,1.0440,0.7400;10,10,11,0.1966,0.065;11,11,12,0.3744,0.1238;12,12,13,1.4680,1.1550;13,13,14,0.5416,0.7129;14,14,15,0.5910,0.5260;15,15,16,0.7463,0.5450;16,16,17,1.2890,1.7210;17,17,18,0.7320,0.5740;18,2, 19,0.1640,0.1565;19,19,20,1.5042,1.3554;20,20,21,0.4095,0.4784;21,21,22,0.7089,0.9373;22,3, 23,0.4512,0.3083;23,23,24,0.8980,0.7091;24,24,25,0.8960,0.7011;25,6, 26,0.2030,0.1034;26,26,27,0.2842,0.1447;27,27,28,1.0590,0.9337;28,28,29,0.8042,0.7006;29,29,30,0.5075,0.2585;30,30,31,0.9744,0.9630;31,31,32,0.3105,0.3619;32,32,33,0.3410,0.5302;];%% 数据初始化[busnum,row]=size(Bus);[branchnum,row]=size(Branch);soubus=Branch(:,2);mobus=Branch(:,3);Vbus=ones(busnum,1);Vbus(:,1)=12.66;Vbus1=Vbus;Ploss=zeros(busnum,1);Qloss=zeros(busnum,1);e=1;k=0;Branch1=Branch;n=1;%% 前推回代循环while ~isempty(Branch1)m=1;[s,row]=size(Branch1);while s>0t=find(Branch1(:,2)== Branch1(s,3));if isempty(t)T1(n,:)= Branch1(s,:);n=n 1;elseT2(m,:)= Branch1(s,:);m=m 1;end;s=s-1;end;Branch1=T2;T2=[];end;while e>1.0e-05P=zeros(busnum,1);Q=zeros(busnum,1);for s=1:branchnumi=T1(s,2);j=T1(s,3);R=T1(s,4);X=T1(s,5);Pload=Bus(j,2);Qload=Bus(j,3);II=((Pload P(j))^2 (Qload Q(j))^2)/(Vbus(j)^2*1000);Ploss(i,j)=II*R;Qloss(i,j)=II*X;P(i,j)=Pload Ploss(i,j) P(j);Q(i,j)=Qload Ploss(i,j) Q(j);P(i)=P(i) P(i,j);Q(i)=Q(i) Q(i,j);end;for s=branchnum:-1:1i=T1(s,2);j=T1(s,3);R=T1(s,4);X=T1(s,5);Vbus(j)=(Vbus(i)-(P(i,j)*R Q(i,j)*X)/(Vbus(i)*1000))^2 ((P(i,j)*X-Q(i,j)*R)/(Vbus(i)*1000))^2;Vbus(j)=sqrt(Vbus(j));end;e=max(abs(Vbus1-Vbus));Vbus1=Vbus;k=k 1;end;%% 输出结果% numc=[1:1:33];% figure;% plot(numc,Vbus1);% xlabel('节点')% ylabel('电压幅值/kv')voltage=Vbus1;end