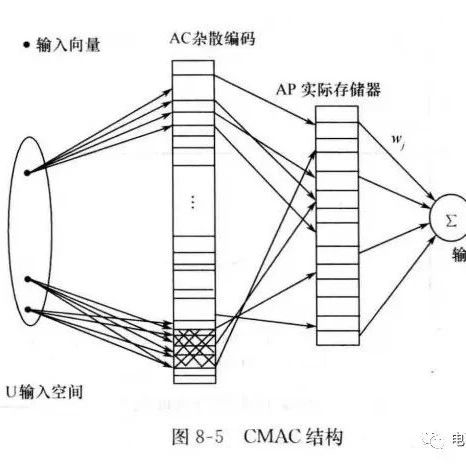
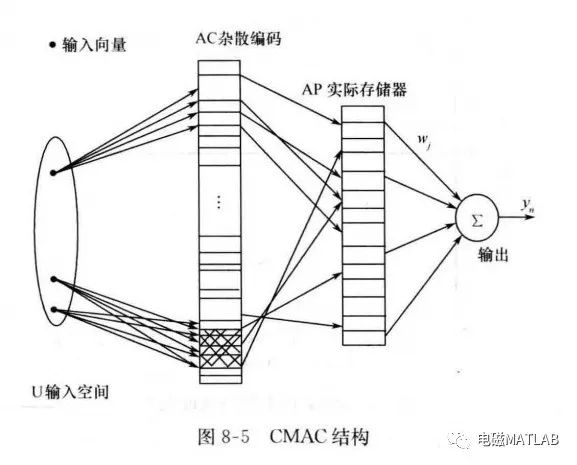
一、灰色预测模型
GM(1.1)模型由包含单一变量的一阶微分方程构成的模型,是灰色模型中最常用的模型。设有负荷变量为的原始数据列:
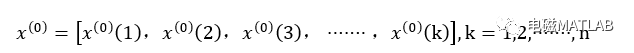
生成一阶累加数据列:
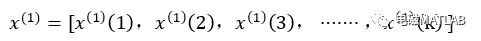
其中
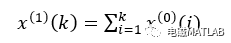
一阶微分方程的解呈指数增长形式,与序列增长规律相同,可认为x(1)序列满足下列方程:
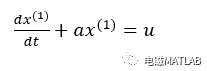
根据导数定义得:
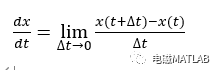
离散形式下,微分项可以表示为:
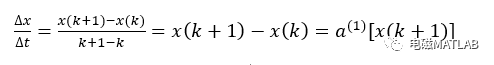
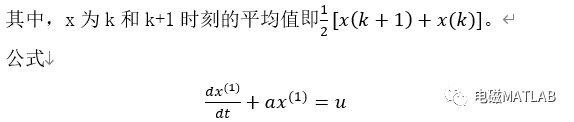
表示:
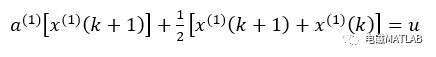
得:
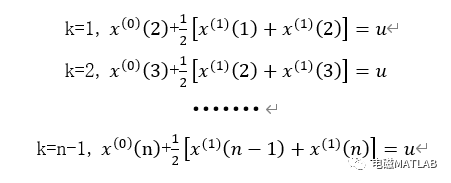
将上述方程用矩阵形式表示为
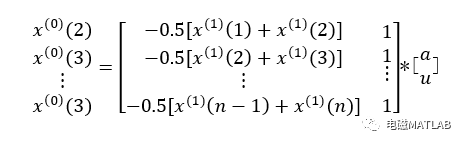
简记为:
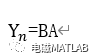
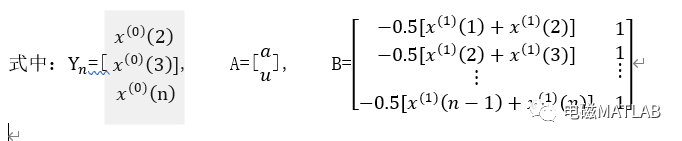
由上述方程可知,和B为已知量,A为待定参数,存在A和u两个变量和n-1个方程,由n-1>2可知,方程组无解。由最小二乘法得到近似解,式=BA可写为
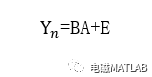
其中,E为误差项
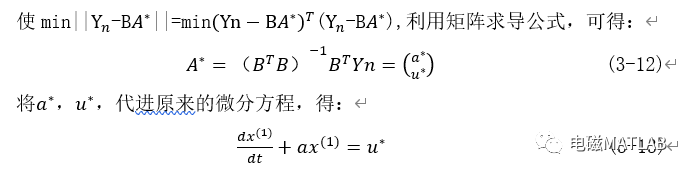
解之可得:

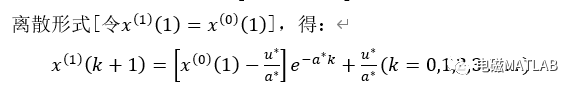
上式称为GM(1,1)模型的时间函数模式,是GM(1,1)模型灰色预测的具体计算公式,对此公式做累减还原,得到原始数列的灰色预测模型为:
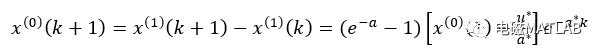
二、算例
以2010-2018年负荷数据作为算例惊醒模型负荷预测
%% 原始数据
%年份。。。。。。。。。。。。。。。。。。。。。。。。。。负荷
S=[2000 4149 1149 2003.07 4851 2396 208.15
2001 4186 1273 2175.68 5221 2500 222.28
2002 4222 1360 2450.48 5829 2651 246.57
2003 4254 1447 2807.41 6624 2739 299.53
2004 4284 1524 3456.7 8097 3353 389.2
2005 4311 1595 4056.76 9440 3821 391.98
2006 4339 1687 4820.53 10679 4117 446.2
2007 4368 1739 5800.25 13322 4676 511.09
2008 4400 1820 6971.05 15900 5805 545.88
2009 4432 1914 7655.18 17335 6212 609.22
2010 4462 1966 9451.26 21253 7989 700.51
2011 4488 2051 11702.82 26150 9523 835.1
2012 4504 2140 12948.88 28800 10573 867.7
2013 4522 2210 14410.19 31930 11910 947.1
2014 4542 2281 15714.63 34674 12000 1018.52
2015 4566 2357 16923.78 36724 14489 1087.26
2016 4592 2438 18499 40400 16040 1182.5
2017 4622 2524 20006.31 43424 17290 1293.98
2018 4648 2604 22716.51 49013 18322 1428.77];
结果:
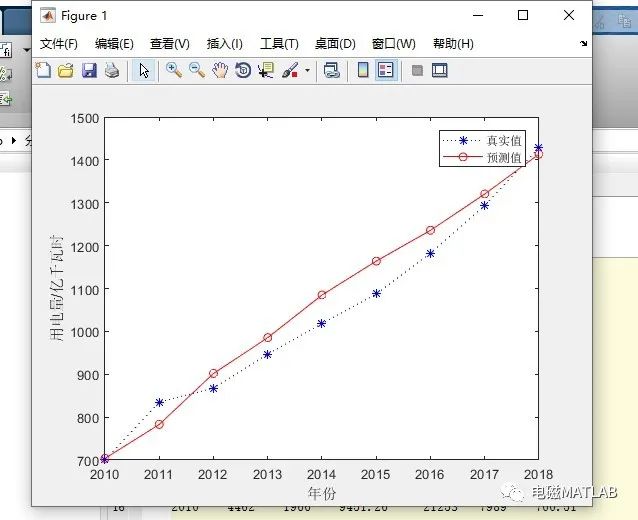
三、matlab程序
// 灰色预测g(1,1)模型,负荷预测clcclose allclear all%% 原始数据%年份。。。。。。。。。。。。。。。。。。。。。。。。。。负荷S=[2000 4149 1149 2003.07 4851 2396 208.152001 4186 1273 2175.68 5221 2500 222.282002 4222 1360 2450.48 5829 2651 246.572003 4254 1447 2807.41 6624 2739 299.532004 4284 1524 3456.7 8097 3353 389.22005 4311 1595 4056.76 9440 3821 391.982006 4339 1687 4820.53 10679 4117 446.22007 4368 1739 5800.25 13322 4676 511.092008 4400 1820 6971.05 15900 5805 545.882009 4432 1914 7655.18 17335 6212 609.222010 4462 1966 9451.26 21253 7989 700.512011 4488 2051 11702.82 26150 9523 835.12012 4504 2140 12948.88 28800 10573 867.72013 4522 2210 14410.19 31930 11910 947.12014 4542 2281 15714.63 34674 12000 1018.522015 4566 2357 16923.78 36724 14489 1087.262016 4592 2438 18499 40400 16040 1182.52017 4622 2524 20006.31 43424 17290 1293.982018 4648 2604 22716.51 49013 18322 1428.77];%% 灰色模型Result2=ones(1,9);E2=ones(1,9);for i=1:9 T=[S(11,7),S(12,7),S(13,7),S(14,7),S(15,7),S(16,7),S(17,7),S(18,7),S(19,7)]; A=[S(i,7),S(i 1,7),S(i 2,7),S(i 3,7),S(i 4,7),S(i 5,7),S(i 6,7),S(i 7,7),S(i 8,7),S(i 9,7)];syms a u;c=[a,u]';Ago=cumsum(A);n=length(A);for k=1:(n-1) Z(k)=(Ago(k) Ago(k 1))/2;endYn =A;%Yn为常数项向量Yn(1)=[]; %从第二个数开始,即x(2),x(3)...Yn=Yn';E=[-Z;ones(1,n-1)]';%累加生成数据做均值c=(E'*E)\(E'*Yn);%利用公式求出a,uc= c';a=c(1);%得到a的值u=c(2);%得到u的值F=[];F(1)=A(1);for k=2:(n 1) F(k)=(A(1)-u/a)/exp(a*(k-1)) u/a;%求出GM(1,1)模型公式endG=[];G(1)=A(1);for k=2:(n 1) G(k)=F(k)-F(k-1);%两者做差还原原序列,得到预测数据endresult=G(11);Result2(i)=result;E2(i)=(result-T(i))/result;end%% 输出figureplot(2010:1:2018,T,'b:*',2010:1:2018,Result2,'r-o')legend('真实值','预测值')xlabel('年份')ylabel('用电量/亿千瓦时')


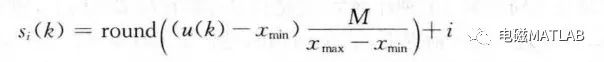






暂无评论