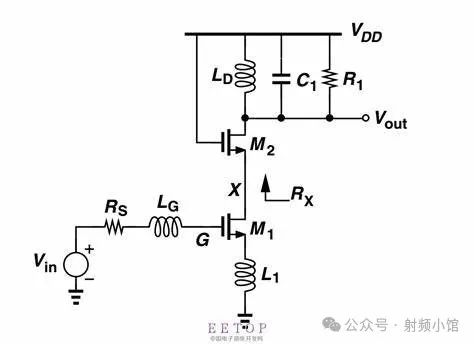
一、理论基础:噪声与增益的辩证关系1.1 Friis公式的启示
根据噪声系数级联公式:
Ftotal=F1 F2−1G1 F3−1G1G2 ⋯
LNA作为第一级(F₁)的增益G₁对系统总噪声起决定性作用。但该公式隐含两个关键前提:
增益临界点现象:当G₁足够大时(通常>15dB),后级噪声贡献可忽略,此时继续提高增益对系统噪声系数无改善。实验数据表明,当LNA增益超过17dB后,系统总噪声系数进入平台期(如原图所示)。
噪声系数与增益的独立性:LNA的噪声系数F₁由晶体管偏置点和输入匹配决定,与增益G₁无直接关联。高增益可能要求更大的偏置电流,反而可能恶化噪声系数。
1.2 SNR与误码率的本质关联
误码率(BER)由信噪比(SNR)直接决定,而SNR的数学表达为:
SNR=SNtotal=GLNA⋅SinGLNA⋅Nin Nadd当LNA增益足够大时,系统噪声由LNA自身噪声主导(N_add≈G_LNA·N_in),此时:SNR≈SinNin Nadd/GLNA→SinNin
这表明:超过临界增益后,SNR不再提升。若盲目增大增益,可能因引入非线性产物(如三阶交调)反而降低有效SNR。二、工程实践中的多维约束2.1 线性度与增益的负相关
晶体管的工作点选择存在根本性矛盾:
高增益模式:需要增大偏置电流以提高跨导,但会导致:
直流功耗上升(违背低功耗设计准则)
输出阻抗降低,恶化线性度(IIP3下降)
实验数据佐证:某LNA在增益从15dB提升至25dB时,IIP3从 5dBm降至-10dBm(如MAX2741案例)。这会显著降低系统抗干扰能力,导致带外阻塞信号通过非线性效应抬高基底噪声。
2.2 稳定性与增益的博弈
根据Rollett稳定性因子K:
K=1−∣S11∣2−∣S22∣2 ∣Δ∣22∣S12S21∣
高增益设计要求S21(正向增益)最大化,但会导致:
稳定性恶化(K<1时可能自激振荡)<>
输入/输出匹配网络复杂度剧增(需引入损耗性元件降Q值)
2.3 带外抑制的连锁反应
高增益LNA会放大前级滤波器的残余带外干扰:
SAW滤波器局限性:典型带外抑制约40-50dB,对GPS等弱信号系统仍可能残留-90dBm干扰
非线性产物危害:例如LTE B2/B3频段的二次谐波通过LNA非线性产生GPS频段交调分量
系统级验证案例:某GPS接收机采用25dB增益LNA时,带外干扰导致C/N0下降8dB;将增益降至16dB后,C/N0恢复至设计值
三、设计方法论:寻找最优平衡点3.1 临界增益的确定
通过噪声系数贡献度分析法确定最小必要增益:
Gmin=10log(Ftotal−F1F2−1) 3dB(安全裕量)
以典型接收链路(LNA→Mixer→IF Amp)为例:
LNA噪声系数F₁=2dB
混频器噪声系数F₂=10dB
代入计算得G_min≈14dB,与厂商建议值(15-17dB)高度吻合
3.2 多参数联合优化策略
采用Pareto最优前沿方法进行参数权衡:
噪声匹配与增益匹配分离设计:通过源极负反馈等技术实现噪声最优输入匹配,输出端通过共轭匹配实现增益最大化
偏置点动态调节:对于多频段系统,可设计自适应偏置电路(如电流镜阵列),在不同频段切换最佳工作点
级间隔离度优化:在LNA与后级间插入衰减器或缓冲级,兼顾增益与稳定性
四、典型案例分析4.1 卫星导航接收机设计
需求矛盾:需要极高灵敏度(-150dBm),但同时面临强带外干扰(如GLONASS L1频段邻近WiFi)
解决方案:
LNA增益设定为16dB(略高于临界值14dB)
采用噪声系数1.2dB的GaAs HEMT
输出端插入3dB衰减器提升IIP3至 8dBm
实测系统灵敏度-148dBm,IIP3优于-15dBm
4.2 5G毫米波前端设计
特殊挑战:高频段损耗大,需要更高增益,但毫米波器件线性度差
创新方法:
采用分布式放大器结构,将总增益拆分为3级(5dB 5dB 6dB)
每级间加入λ/4微带线提升隔离度
最终实现16dB增益,NF=3.5dB,IIP3=-5dBm
五、结论
LNA增益的优化本质上是多约束条件下的最优化问题:
理论层面:存在明确的增益临界值,超过该值后系统性能不再提升
工程层面:需综合考虑噪声、线性度、稳定性、功耗等参数,通过系统级仿真和实测确定最佳工作点
技术趋势:新型材料(如GaN)、电路架构(如Doherty LNA)和智能算法(如ML驱动的参数优化)正在突破传统设计边界,但基础物理规律(噪声与线性度的根本矛盾)仍构成设计约束
最终设计准则可归纳为:在保证系统噪声系数达标的前提下,选择能满足线性度指标的最低增益值。这一原则在卫星通信、雷达、5G等高频系统中已得到充分验证。













暂无评论