(1) 前言

在看完匹配滤波器以后，又冒出来一个新名词，Ambiguity Function。

本来还深吸一口气，准备被虐千百遍。但是仔细往下一看，哦，原来[1]中的Ambiguity function还是和匹配滤波器的输出相关。

顿时放松了很多。

(2) 什么是Ambiguity function?

Ambiguity function，中文翻译过来是，模糊函数。

假设匹配滤波器是针对波形x(t)设计的，而匹配滤波器的输入是计入了多普勒频移的回波，不过这里，还是忽略了总时延[1]，如下图所示。

匹配滤波器的输出，称为复模糊函数(complex ambiguity function)，而复模糊函数的幅度，称为模糊函数(Ambiguity function)。

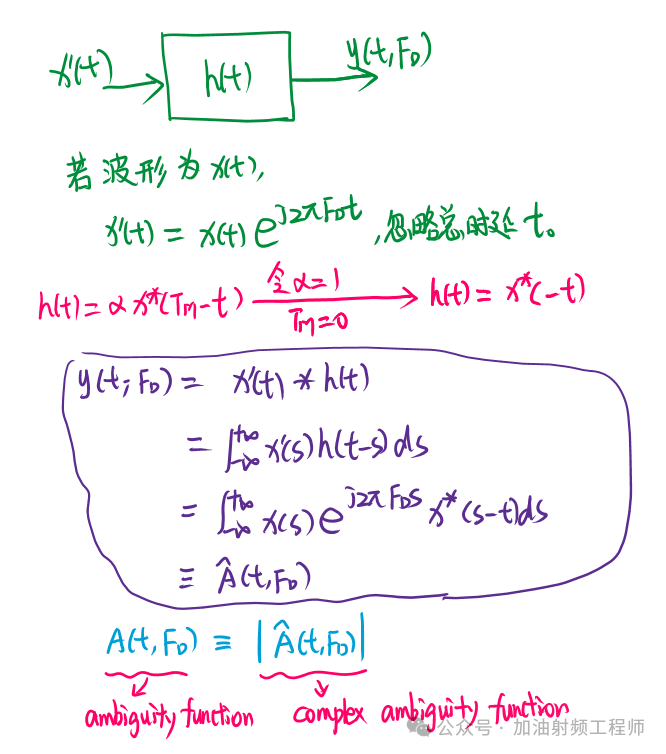
模糊函数，有两个维度，一个是t，即时延，对应距离；另一个时FD，即多普勒频移，对应速度。

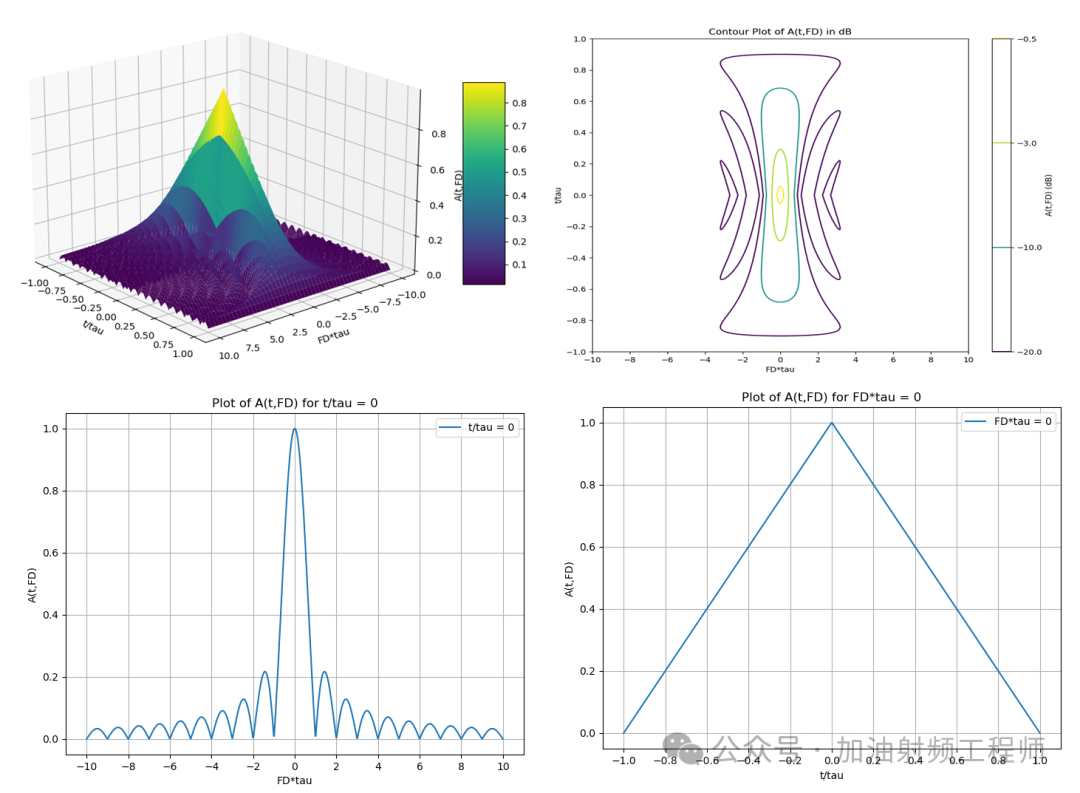
所以，模糊函数可以用来分析雷达波形的距离和速度的分辨率，从而确定波形是否适合相应场景下的应用。

(3) 简单脉冲的模糊函数

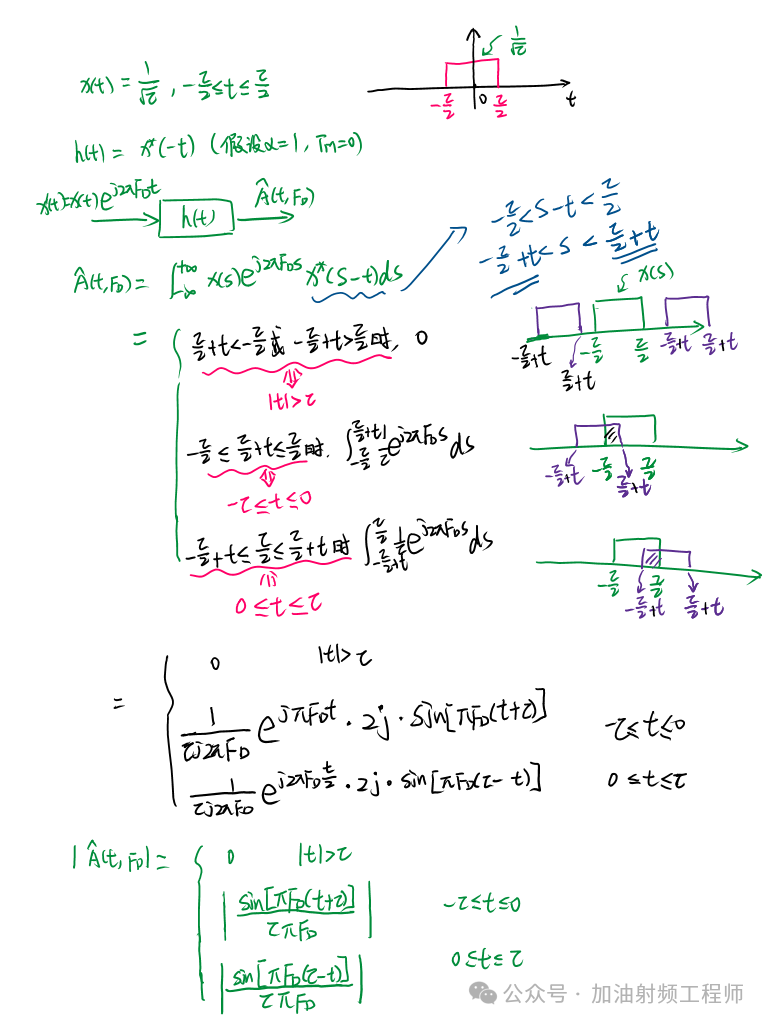
简单脉冲波形，如下图所示，为了计算方便，幅度进行了归一化处理，使得波形的能量E=1。其模糊函数的推导如下：

#绘制三维图%matplotlib qtimport numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3D



# 创建 x 和 y 的值tdivtau = np.linspace(-1, 1, 1000)Ftau = np.linspace(-10, 10, 1000)t,F  = np.meshgrid(tdivtau, Ftau)

# 计算 z 的值Z = np.abs(np.sinc(F*(1-np.abs(t)))*(1-np.abs(t)))



# 创建三维图形fig = plt.figure(figsize=(12,8))ax = fig.add_subplot(111, projection='3d')

# 绘制三维曲面surf=ax.plot_surface(t, F, Z, cmap='viridis',edgecolor='none',antialiased=True)

# 翻转 x 轴ax.invert_xaxis()

# 设置标签ax.set_xlabel('t/tau')ax.set_ylabel('FD*tau')ax.set_zlabel('A(t,FD)')

# 添加颜色条以显示 Z 值的映射关系fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

# 调整视角ax.view_init(elev=20, azim=140)  # 改变 elev 和 azim 参数以调整视角



# 显示图形plt.show()

#绘制等高线import numpy as npimport matplotlib.pyplot as plt

# 创建 x 和 y 的值tdivtau = np.linspace(-1, 1, 1000)Ftau = np.linspace(-10, 10, 1000)t, F = np.meshgrid(tdivtau, Ftau)

# 计算原始函数的值A_original = np.abs(np.sinc(F*(1-np.abs(t)))*(1-np.abs(t)))

# 将函数转换为 dB 单位（20*log10()）A_dB = 20 * np.log10(A_original)

# 绘制等高线图plt.figure(figsize=(10, 8))

# 绘制指定 dB 值的等高线contour_plot = plt.contour(F, t, A_dB, levels=[-20, -10, -3, -0.5], cmap='viridis')

# 添加颜色条plt.colorbar(contour_plot, label='A(t,FD) (dB)')

# 设置标签和标题plt.xlabel('FD*tau')plt.ylabel('t/tau')plt.xticks(np.arange(-10, 11, step=2))plt.yticks(np.arange(-1, 1.1, step=0.2))plt.title('Contour Plot of A(t,FD) in dB')

# 显示图形plt.show()

#绘制Zero_delay截面图import numpy as npimport matplotlib.pyplot as plt

# 创建 F 的值Ftau = np.linspace(-10, 10, 1000)

# 设置 t 为常数t = 0

# 计算 Z 的值Z = np.abs(np.sinc(Ftau*(1-np.abs(t)))*(1-np.abs(t)))

# 绘制二维函数图plt.figure(figsize=(8, 6))plt.plot(Ftau, Z, label=f't/tau = {t}')plt.xlabel('FD*tau')plt.ylabel('A(t,FD)')plt.title('Plot of A(t,FD) for t/tau = 0')

plt.xticks(np.arange(-10,11,step=2))plt.legend()plt.grid(True)plt.show()

#绘制Zero_Doppler截面图import numpy as npimport matplotlib.pyplot as plt

# 设置 F 为常数Ftau = 0

# 设置tt = np.linspace(-1, 1, 1000)

# 计算 Z 的值Z = np.abs(np.sinc(Ftau*(1-np.abs(t)))*(1-np.abs(t)))

# 绘制二维函数图plt.figure(figsize=(8, 6))plt.plot(t, Z, label=f'FD*tau = {Ftau}')plt.xlabel('t/tau')plt.ylabel('A(t,FD)')plt.title('Plot of A(t,FD) for FD*tau = 0')

plt.xticks(np.arange(-1,1.1,step=0.2))plt.legend()plt.grid(True)plt.show()