一个layout工程师学习信号完整性之路
大家常用于信号完整性仿真的软件主要有Cadence Sigrity、ADS、Ansys、CST等,本人比较常用的有PowerSI、PowerDC、SystemSI、HFSS 3D Layout、ADS等。不同的软件可以组合使用查看时域波形或者眼图之类的。但是每个软件有自己的优点和算法,也决定了其应用的领域,今天简单整理了不同软件的算法,因为毕竟自己经常使用,要知道它是怎么计算和分割我们的PCB板。但是如果要熟悉和理解那可能还要和原厂沟通,因为这个背后的算法还是非常的复杂的。下面简单介绍一下:
一、仿真软件算法介绍:
针对于信号完整性仿真,从仿真的算法来看可以分为六类:MOM(距量)、FDTD(时域有限差分)、FEM(有限元)、BEM(边界元)、FDID(时域有限积分)。
1.MOM(距量):ADS
(2.5D求解器,Power SI中的Model Extraction)矩量法的基本思想是将几何目标剖分离散,在其上定义合适的基函数,然后建立积分方程,用权函数检验从而产生一个矩阵方程,求解改矩阵方程,即可得到几何目标上的电流分布,从而其他近远场信息可从该电流分布求得。适用于天线建模、线建模和表面建模、导线结构的问题。但在非均匀媒介质中会遇到困难,要用大量的内部资源,适用于低频。
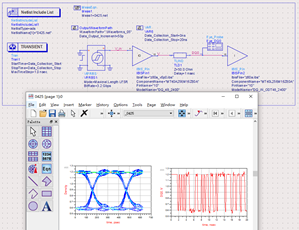
2.FDTD(时域有限差分):CST、Sigrity SPEED 2000
(3D求解器)FDTD 的网格是划分正立方体,用有限差分式替代时域麦克斯韦旋度方程中的微分式,得到关于场分量的有限差分式,针对不同的研究对象,可在不同的坐标系中建模,因而具有这几个优点,容易对复杂媒体建模,通过一次时域分析计算,借助傅里叶变换可以得到整个同带范围内的频率响应;能够实时在现场的空间分布,精确模拟各种辐射体和散射体的辐射特性和散射特性;计算时间短。但是FDTD分析方法由于受到计算机存储容量的限制,其网格空间不能无限制的增加,造成FDTD方法不能适用于较大尺寸,也不能适用于细薄结构的媒质。因为这种细薄结构的最小尺寸比FDTD网格尺寸小很多,若用网格拟和这类细薄结构只能减小网格尺寸,而这必然导致计算机存储容量的加大。
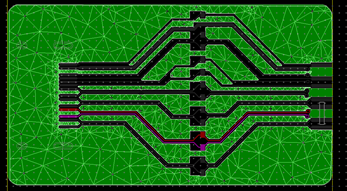
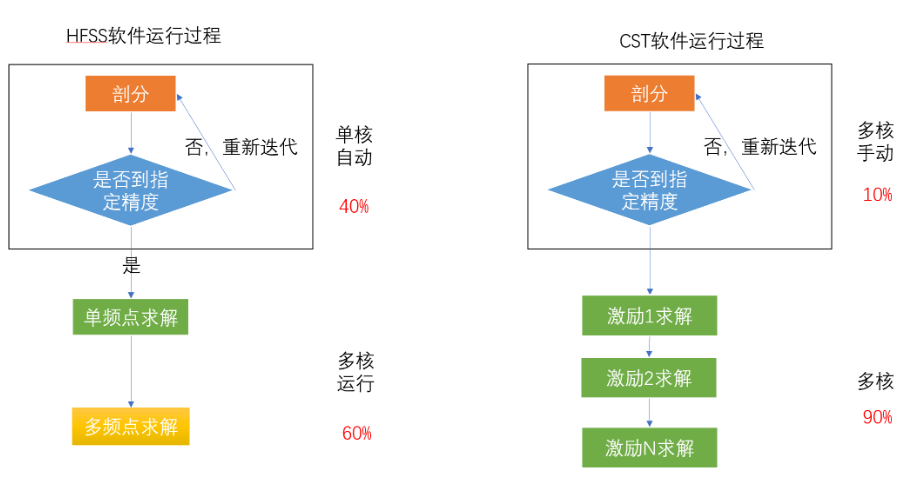
3.FEM(有限元):HFSS、ADS、 Sigrity 3DFEM,
(3D求解器)有限元法(FEM,Finite Element Method)是一种为求解偏微分方程边值问题近似解的数值技术。求解时对整个问题区域进行分解,每个子区域都成为简单的部分,这种简单部分就称作有限元。
它通过变分方法,使得误差函数达到最小值并产生稳定解。类比于连接多段微小直线逼近圆的思想,有限元法包含了一切可能的方法,这些方法将许多被称为有限元的小区域上的简单方程联系起来,并用其去估计更大区域上的复杂方程。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。第一步:区域离散化,第二步:选择插值函数,第三步:方程组公式建立,第四步:选择合适的代数解法求解代数方程,即可得到待求解边值问题的数值解。

4.BEM(边界元):
边界元法(boundary element method)是一种继有限元法之后发展起来的一种新数值方法,与有限元法在连续体域内划分单元的基本思想不同,边界元法是只在定义域的边界上划分单元,用满足控制方程的函数去逼近边界条件。所以边界元法与有限元相比,具有单元个数少,数据准备简单等优点。但用边界元法解非线性问题时,遇到同非线性项相对应的区域积分,这种积分在奇异点附近有强烈的奇异性,使求解遇到困难
5.FDID(时域有限积分):CST
(3D求解器)有限积分法属于全波分析方法,可以处理任意结构、任意材料的物体。
6.多层快速多极子算法:CST
其算法是处理物体的面网格,对物体不是进行体网格剖分,只是在物体的表面划分网格,这决定了它在处理复杂物体的不足,但是在解决结构简单的物体是很有效,可以与有限积分互补。
以上资料主要是本人在仿真流程中和网络搜索整理而成
如有雷同或错误,希望各位大神留言指正,感谢!!!







暂无评论