交—直—交变频器、不间断电源、开关电源等应用场合大都采用不可控整流电路。最常用的是单相桥式和三相桥式两种接法，由于电路中的电力电子器件采用整流二极管，故也称这类电路为二极管整流电路。01电容滤波的单相不可控整流电路

首先，我们先介绍电容滤波的单相不可控整流电路，下面是其基本的电路拓扑和工作波形：

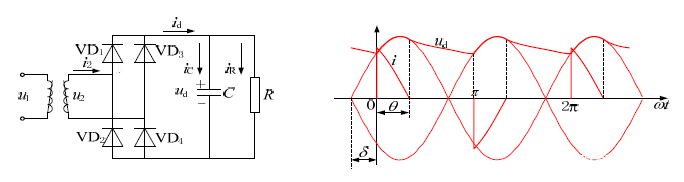
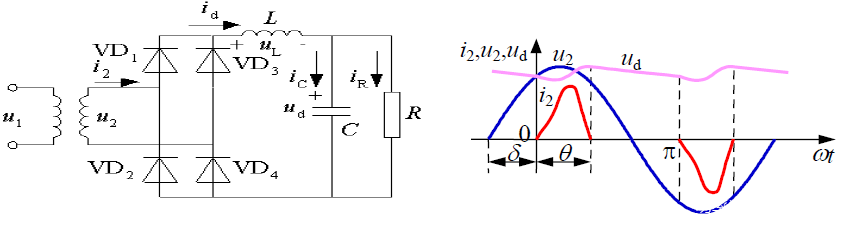
电容滤波的单相桥式不可控整流电路及其工作波形

工作原理及波形分析

基本工作过程

在u2正半周过零点至ωt=0期间，因u2d，故二极管均不导通，此阶段电容C向R放电，提供负载所需电流，同时ud下降。至ωt=0之后，u2将要超过ud，使得VD1和VD4开通，ud=u2，交流电源向电容充电，同时向负载R供电。电容被充电到ωt=θ时，ud=u2 ，VD1和VD4关断。电容开始以时间常数RC 按指数函数放电。当ωt=π，即放电经过π-θ角时，ud降至开始充电时的初值，另一对二极管VD2和VD3导通，此后u2又向C充电，与u2正半周的情况一样。

δ和θ的确定

δ指VD1和VD4导通的时刻与u2过零点相距的角度，θ指VD1和VD4的导通角。在VD1和VD4导通期间

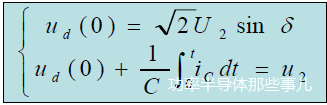
式中，ud(0)为VD1、VD4开始导通时刻直流侧电压值。将u2代入并求解得：

于是

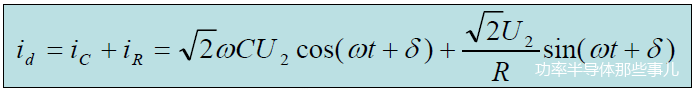
则当ωt=θ时，VD1和VD4关断。将id(θ)=0代入上式，得：

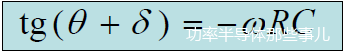
二极管导通后u2开始向C充电时的ud与二极管关断后C放电结束时的ud相等，故有下式成立：

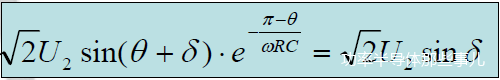
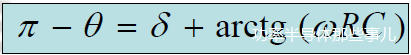
由上式得

显然θ和δ仅由乘积ωRC决定。

θ和δ与ωRC的关系曲线

主要的数量关系

输出电压平均值

空载时，Ud=√2U2

重载时，Ud逐渐趋近于0.9U2，即趋近于接近电阻负载时的特性。

在设计时根据负载的情况选择电容C值，使RC≥(3~5)T/2 , 此时输出电压为：

电流平均值

输出电流平均值IR和二极管电流iD平均值为：

二极管承受的电压

为变压器二次侧电压最大值，即√2U2。

感容滤波的单相桥式不可控整流电路

实际应用中为了抑制电流冲击，常在直流侧串入较小的电感。ud波形更平直，电流i2的上升段平缓了许多，这对于电路的工作是有利的。

感容滤波的单相桥式不可控整流电路及其工作波形

02电容滤波的三相不可控整流电路

我们再来介绍电容滤波的三相不可控整流电路，下面是其基本的电路拓扑和工作波形：

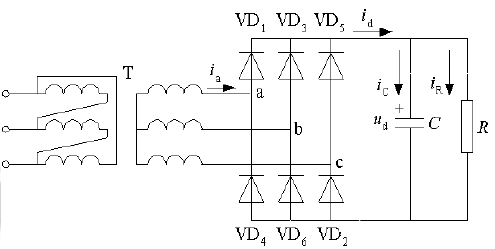
电容滤波的三相桥式不可控整流电路

工作波形

基本原理

当某一对二极管导通时，输出直流电压等于交流侧线电压中最大的一个， 该线电压既向电容供电，也向负载供电。当没有二极管导通时，由电容向负载放电，ud按指数规律下降。

电流id断续和连续

比如在VD1和VD2同时导通之前VD6和VD1是关断的，交流侧向直流侧的充电电流id是断续的。VD1一直导通，交替时由VD6导通换相至VD2导通，id是连续的。

由“电压下降速度相等”的原则，可以确定临界条件，假设在ωt δ=2π/3的时刻“速度相等”恰好发生，则有

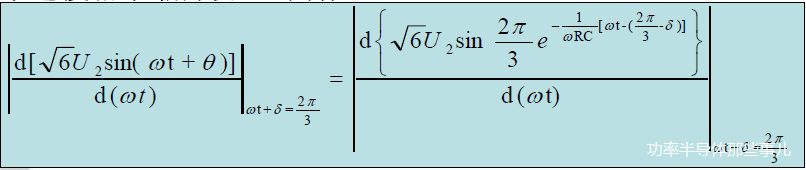
可得ωRC=√3，这就是临界条件。ωRC>√3和ωRC<<>√3分别是电流id断续和连续的条件。通常只有R是可变的，它的大小反映了负载的轻重，因此在轻载时直流侧获得的充电电流是断续的，重载时是连续的。

考虑电感

实际电路中存在交流侧电感以及为抑制冲击电流而串联的电感。有电感时，电流波形的前沿平缓了许多，有利于电路的正常工作。随着负载的加重，电流波形与电阻负载时的交流侧电流波形逐渐接近。

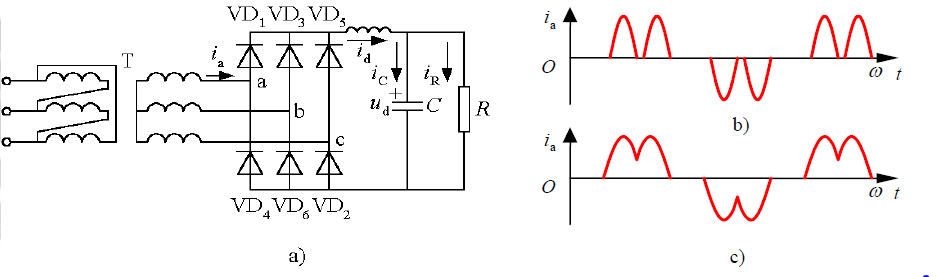
考虑电感时电容滤波的三相桥式整流电路及其波形 

b)轻载时的交流侧电流波形c)重载时的交流侧电流波形

主要数量关系

输出电压平均值

Ud在（2.34U2 ~2.45U2）之间变化。

电流平均值

输出电流平均值IR为：IR=Ud/R

电容电流iC平均值为零，因此：Id=IR

二极管电流平均值为Id的1/3，即ID=Id/3=IR/3

二极管承受的电压

为线电压的峰值，即√6U2。

以上便是含有滤波电容的单相和三相整流电路的原理分析和数量关系，滤波电容的存在主要是起到一个“水缸”的作用，使得整流电路的波形更加平滑。